"Westgard Rules"

See the power functions of the different controls rules and combinations of multirules that make up the "Westgard Rule"

This article is exclusively sponsored by LGC Technopath Clinical Diagnostics

POWER FUNCTION GRAPHS

• Ns of 2 for systematic error
• Ns of 2 for random error
• Ns of 4 for systematic error
• Ns of 4 for random error

The rationale for using multirule procedures and the expected performance characteristics of Westgard rules can be shown by power function graphs. See the lesson on Power Function Graphs for more background information and a better understanding of statistical power, power curves, and power function graphs.

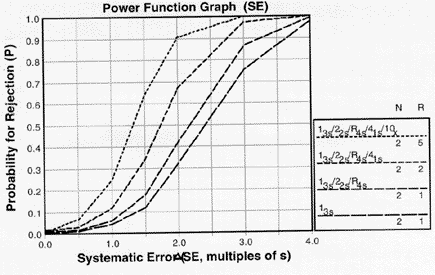
Ns of 2 for systematic error

The accompanying figure shows a power function graph for systematic error, i.e., the probability of rejection on the y-axis versus the size of systematic error on the x-axis. Think of a 2s SE as a systematic shift equivalent to 2 times the SD of the method.

When N=2, the error detection available from a 1_3s control rule is shown by the bottom power curve. The increase in power from adding the 2_2s and R_4s rules is shown by the second curve from the bottom. Use of the 4_1s rule to "look-back" over two consecutive runs provides additional detection of persistent systematic errors, as shown by the next to the top curve ( for N=2, R=2). This can be further increased when the 10_x is used to look-back over five consecutive runs (top curve, R=5).

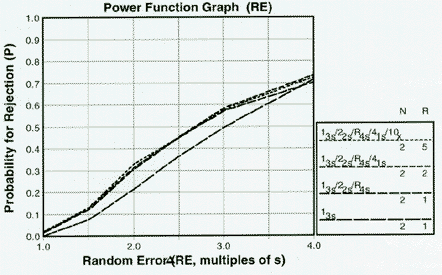
Ns of 2 for random error

The power function for random error again shows the probability for rejection on the y-axis versus increases in random error on the x-axis. Think of an RE of 2.0 as a doubling of the SD of the method.

Random error is detected mainly by the 1_3s and R_4s rules. We have recommended that rules for random error, such as R_4s, be used only within a run in order to distinguish random error from between run systematic errors (which should be detected by rules such as 4_1s, 10_x). Therefore, the power of the multirule combinations show no further improvements in detection of random errors for across run applications; the power curves for the R-2 and R=5 combinations that use the 1_3s and R_4s rules essentially coincide with the power curve for those rules with R=1, as shown by the top three curves on this power function graph.

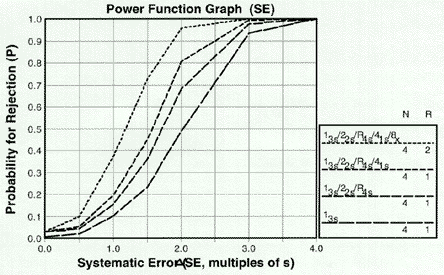
Ns of 4 for systematic error

Further improvements in error detection can be expected when N is increased to 4 because the 1_3s, 2_2s, R_4s, and 4_1s can now all be applied within the run.

For detection of systematic errors, the original error detection of the 1_3s control rule is shown by the bottom power curve, the increase from addition of the 2_2s and R_4s rules is shown by the next to bottom curve, and the increase from use of the 4_1s rule within run is shown by the next to top curve. Error detection across runs is increased by the use of the 8_x rule to look-back over two consecutive runs (N=4, R=2).

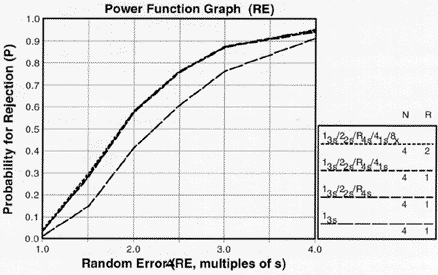
Ns of 4 for random error

The detection of random error is again affected primarily by the 1_3s and R_4s rules. The original error detection from the 1_3s rule is shown by the bottom curve and is increased by the addition of the R_4s rule as shown by the top curves.