Z-Stats / Basic Statistics

Don't be caught in your skivvies when you talk about CV's, or confuse STD's with SD's. Do you know what they mean when they talk about mean? These are the bread and butter statistical calculations. Make sure you're doing them right.

EdD Assistant Professor
Clinical Laboratory Science Program University of Louisville
Louisville, Kentucky
June 1999

• Mean or average
• Standard deviation
• Degrees of freedom
• Variance
• Normal distribution
• Coefficient of variation
• Alternate formulae
• References
• Self-assessment exercises
• About the Author

Many of the terms covered in this lesson are also found in the lessons on Basic QC Practices, which appear on this website. It is highly recommended that you study these lessons online or in hard copy[1]. The importance of this current lesson, however, resides in the process. The lesson sets up a pattern to be followed in future lessons.

Mean or average

The simplest statistic is the mean or average. Years ago, when laboratories were beginning to assay controls, it was easy to calculate a mean and use that value as the "target" to be achieved. For example, given the following ten analyses of a control material - 90, 91, 89, 84, 88, 93, 80, 90, 85, 87 - the mean or Xbar is 877/10 or 87.7. [The term Xbar refers to a symbol having a line or bar over the X,, however, we will use the term instead of the symbol in the text of these lessons because it is easier to present.]

The mean value characterizes the "central tendency" or "location" of the data. Although the mean is the value most likely to be observed, many of the actual values are different than the mean. When assaying control materials, it is obvious that technologists will not achieve the mean value each and every time a control is analyzed. The values observed will show a dispersion or distribution about the mean, and this distribution needs to be characterized to set a range of acceptable control values.

Standard deviation

The dispersion of values about the mean is predictable and can be characterized mathematically through a series of manipulations, as illustrated below, where the individual x-values are shown in column A.

Column A	Column B	Column C
X value	X value-Xbar	(X-Xbar)2
90	90 - 87.7 = 2.30	(2.30)2 = 5.29
91	91 - 87.7 = 3.30	(3.30)2 = 10.89
89	89 - 87.7 = 1.30	(1.30)2 = 1.69
84	84 - 87.7 = -3.70	(-3.70)2 = 13.69
88	88 - 87.7 = 0.30	(0.30)2 = 0.09
93	93 - 87.7 = 5.30	(5.30)2 = 28.09
80	80 - 87.7 = -7.70	(-7.70)2 = 59.29
90	90 - 87.7 = 2.30	(2.30)2 = 5.29
85	85 - 87.7 = -2.70	(-2.70)2 = 7.29
87	87 - 87.7 = -0.70	(-0.70)2 = 0.49
X = 877	(X-Xbar) = 0	(X-Xbar)² = 132.10

• The first mathematical manipulation is to sum (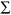) the individual points and calculate the mean or average, which is 877 divided by 10, or 87.7 in this example.
• The second manipulation is to subtract the mean value from each control value, as shown in column B. This term, shown as X value - Xbar, is called the difference score. As can be seen here, individual difference scores can be positive or negative and the sum of the difference scores is always zero.
• The third manipulation is to square the difference score to make all the terms positive, as shown in Column C.
• Next the squared difference scores are summed.
• Finally, the predictable dispersion or standard deviation (SD or s) can be calculated as follows:

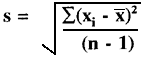
= [132.10/(10-1)]1/2 = 3.83

Degrees of freedom

The "n-1" term in the above expression represents the degrees of freedom (df). Loosely interpreted, the term "degrees of freedom" indicates how much freedom or independence there is within a group of numbers. For example, if you were to sum four numbers to get a total, you have the freedom to select any numbers you like. However, if the sum of the four numbers is stipulated to be 92, the choice of the first 3 numbers is fairly free (as long as they are low numbers), but the last choice is restricted by the condition that the sum must equal 92. For example, if the first three numbers chosen at random are 28, 18, and 36, these numbers add up to 82, which is 10 short of the goal. For the last number there is no freedom of choice. The number 10 must be selected to make the sum come out to 92. Therefore, the degrees of freedom have been limited by 1 and only n-1 degrees of freedom remain. In the SD formula, the degrees of freedom are n minus 1 because the mean of the data has already been calculated (which imposes one condition or restriction on the data set).

Variance

Another statistical term that is related to the distribution is the variance, which is the standard deviation squared (variance = SD² ). The SD may be either positive or negative in value because it is calculated as a square root, which can be either positive or negative. By squaring the SD, the problem of signs is eliminated. One common application of the variance is its use in the F-test to compare the variance of two methods and determine whether there is a statistically significant difference in the imprecision between the methods.

In many applications, however, the SD is often preferred because it is expressed in the same concentration units as the data. Using the SD, it is possible to predict the range of control values that should be observed if the method remains stable. As discussed in an earlier lesson, laboratorians often use the SD to impose "gates" on the expected normal distribution of control values.

Normal or Gaussian distribution

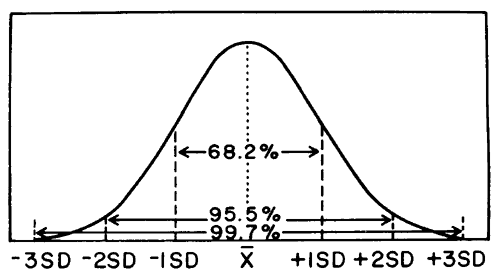Traditionally, after the discussion of the mean, standard deviation, degrees of freedom, and variance, the next step was to describe the normal distribution (a frequency polygon) in terms of the standard deviation "gates." The figure here is a representation of the frequency distribution of a large set of laboratory values obtained by measuring a single control material. This distribution shows the shape of a normal curve. Note that a "gate" consisting of ±1SD accounts for 68% of the distribution or 68% of the area under the curve, ±2SD accounts for 95% and ±3SD accounts for >99%. At ±2SD, 95% of the distribution is inside the "gates," 2.5% of the distribution is in the lower or left tail, and the same amount (2.5%) is present in the upper tail. Some authors call this polygon an error curve to illustrate that small errors from the mean occur more frequently than large ones. Other authors refer to this curve as a probability distribution.

Coefficient of variation

Another way to describe the variation of a test is calculate the coefficient of variation, or CV. The CV expresses the variation as a percentage of the mean, and is calculated as follows:

CV% = (SD/Xbar)100

In the laboratory, the CV is preferred when the SD increases in proportion to concentration. For example, the data from a replication experiment may show an SD of 4 units at a concentration of 100 units and an SD of 8 units at a concentration of 200 units. The CVs are 4.0% at both levels and the CV is more useful than the SD for describing method performance at concentrations in between. However, not all tests will demonstrate imprecision that is constant in terms of CV. For some tests, the SD may be constant over the analytical range.

The CV also provides a general "feeling" about the performance of a method. CVs of 5% or less generally give us a feeling of good method performance, whereas CVs of 10% and higher sound bad. However, you should look carefully at the mean value before judging a CV. At very low concentrations, the CV may be high and at high concentrations the CV may be low. For example, a bilirubin test with an SD of 0.1 mg/dL at a mean value of 0.5 mg/dL has a CV of 20%, whereas an SD of 1.0 mg/dL at a concentration of 20 mg/dL corresponds to a CV of 5.0%.

Alternate formulae

The lessons on Basic QC Practices cover these same terms (see QC - The data calculations), but use a different form of the equation for calculating cumulative or lot-to-date means and SDs. Guidelines in the literature recommend that cumulative means and SDs be used in calculating control limits [2-4], therefore it is important to be able to perform these calculations.

The cumulative mean can be expressed as Xbar = (x_i)_t /n_t, which appears similar to the prior mean term except for the "t" subscripts, which refer to data from different time periods. The idea is to add the x_i and n terms from groups of data in order to calculate the mean of the combined groups.
The cumulative or lot-to-date standard deviation can be expressed as follows:

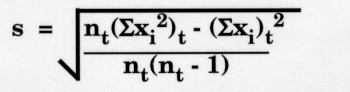
This equation looks quite different from the prior equation in this lesson, but in reality, it is equivalent. The cumulative standard deviation formula is derived from an SD formula called the Raw Score Formula. Instead of first calculating the mean or Xbar, the Raw Score Formula calculates Xbar inside the square root sign.

Oftentimes in reading about statistics, an unfamiliar formula may be presented. You should realize that the mathematics in statistics is often redundant. Each procedure builds upon the previous procedure. Formulae that seem to be different are derived from mathematical manipulations of standard expressions with which you are often already acquainted.

References

1. Westgard JO, Barry, PL, Quam EF. Basic QC practices: Training in statistical quality control for healthcare laboratories. Madison, WI: Westgard Quality Corporation, 1998.
2. Westgard JO, Barry PL, Hunt MR, Groth, T. A multirule Shewhart chart for quality control in clinical chemistry. Clin Chem 1981;27:493-501.
3. Westgard JO, Klee GG. Quality Management. Chapter 17 in Tietz Textbook of Clinical Chemistry, 3rd ed., Burtis and Ashwood, eds. Philadelphia, PA: Saunders, 1999.
4. NCCLS C24-A2 document. Statistical quality control for quantitative measurements: Principles and definitions. National Committee for Clinical Laboratory Standards, Wayne PA, 1999.

Self-assessment exercises

1. Manually calculate the mean, SD, and CV for the following data: 44, 47, 48, 43, 48.
2. Use the SD Calculator to calculate the mean, SD, and CV for the following data: 203, 202, 204, 201, 197, 200, 198, 196, 206, 198, 196, 192, 205, 190, 207, 198, 201, 195, 209, 186.
3. If the data above were for a cholesterol control material, calculate the control limits that would contain 95% of the expected values.
4. If control limits (or SD "gates") were set as the mean +/- 2.5 SD, what percentage of the control values are expected to exceed these limits? [Hint: you need to find a table of areas under a normal curve.]
5. Describe how to calculate cumulative control limits.
6. (Optional) Show the equivalence of the regular SD formula and the Raw Score formula. [Hint: start with the regular formula, substitute a summation term for Xbar, multiply both sides by n/n, then rearrange.]

About the author: Madelon F. Zady

Madelon F. Zady is an Assistant Professor at the University of Louisville, School of Allied Health Sciences Clinical Laboratory Science program and has over 30 years experience in teaching. She holds BS, MAT and EdD degrees from the University of Louisville, has taken other advanced course work from the School of Medicine and School of Education, and also advanced courses in statistics. She is a registered MT(ASCP) and a credentialed CLS(NCA) and has worked part-time as a bench technologist for 14 years. She is a member of the: American Society for Clinical Laboratory Science, Kentucky State Society for Clinical Laboratory Science, American Educational Research Association, and the National Science Teachers Association. Her teaching areas are clinical chemistry and statistics. Her research areas are metacognition and learning theory.