"Westgard Rules" and Multirules
What are the "Westgard Rules"? How do you use them?
Everything you ever wanted to know (or possibly didn't) about multirule QC.
Multirules are popularly known in the laboratory as "Westgard Rules."
Here's the best place to find out more about them.
"Westgard Rules" and Multirule Quality Control
- What is Multirule QC
- What are the "Westgard Rules"?
- What are other common multirules?
- How do you perform multirule QC?
- What is N?
- Why use a multirule QC procedure?
- Are there similar strategies for QC testing and diagnostic testing?
- Are there similar performance characteristics for QC and diagnostic tests?
- How can you use multiple tests to optimize performance?
- When should you use a multirule QC procedure?
Looking for "Westgard Rules" worksheets? Click here
What is a multirule QC procedure?
First, a non-technical description. When my daughter Kristin was young and living at home, she liked to party. One day when she told me she was again intending to be out late, I felt the need to exert some parental control over her hours. So I told her that if she was out once after three, twice after two, or four times after one, she was in big trouble. That's multirule control.
Kristin hates it when I tell this story, and while it isn't entirely true, it's still a good story and makes multirule QC understandable to everyone. (By the way, she turned out okay; she graduated number 1 in her class from law school and I'm very proud of her. It's also true that she has her mother's brains, which together with my persistence - or stubborness, as it's known around the house - makes a pretty good combination.) I will also have to admit that around our house it is Mrs. Westgard's rules that really count. My wife Joan hates it when I tell this part of the story, but she's put up with me for over thirty-five years and I'm now in a state of fairly stable control, so it will take a bigger deviation than this before I get into big trouble.

Now for a more technical description. Multirule QC uses a combination of decision criteria, or control rules, to decide whether an analyticalrun is in-control or out-of-control. The well-known Westgard multirule QC procedure uses 5 different control rules to judge the acceptability of an analytical run. By comparison, a single-rule QC procedure uses a single criterion or single set of control limits, such as a Levey-Jennings chart with control limits set as either the mean plus or minus 2 standard deviations (2s) or the mean plus or minus 3s. "Westgard rules" are generally used with 2 or 4 control measurements per run, which means they are appropriate when two different control materials are measured 1 or 2 times per material, which is the case in many chemistry applications. Some alternative control rules are more suitable when three control materials are analyzed, which is common for applications in hematology, coagulation, and immunoassays.
What are the "Westgard rules"?
For convenience, we adopt a short hand notation to abbreviate different decision criteria or control rules, e.g., 12s to indicate 1 control measurement exceeding 2s control limits. We prefer to use subscripts to indicate the control limits, but other texts and papers may use somewhat different notation (e.g. 1:2s rather than 12s) Combinations of rules are generally indicated by using a "slash" mark (/) between control rules, e.g. 13s/22s.
The individual rule are defined below. The "thumbnail" graphic next to a rule shows an example of control results that violate that rule. You can click on a graphic to get a larger picture that more clearly illustrates the application of each control rule.
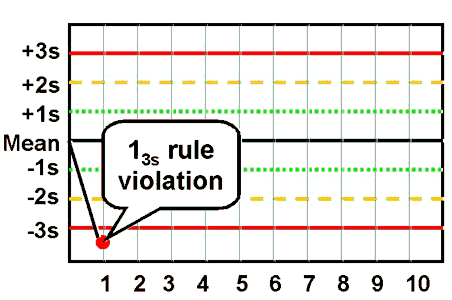
| 13s refers to a control rule that is commonly used with a Levey-Jennings chart when the control limits are set as the mean plus 3s and the mean minus 3s. A run is rejected when a single control measurement exceeds the mean plus 3s or the mean minus 3s control limit.
|
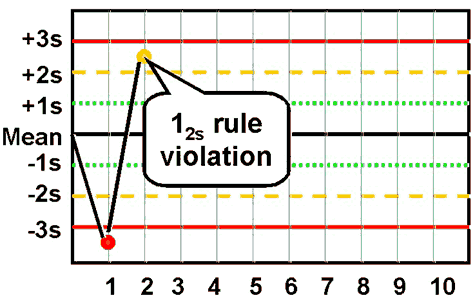
| 12srefers to the control rule that is commonly used with a Levey-Jennings chart when the control limits are set as the mean plus/minus 2s. In the original Westgard multirule QC procedure, this rule is used as a warning rule to trigger careful inspection of the control data by the following rejection rules.
|
|
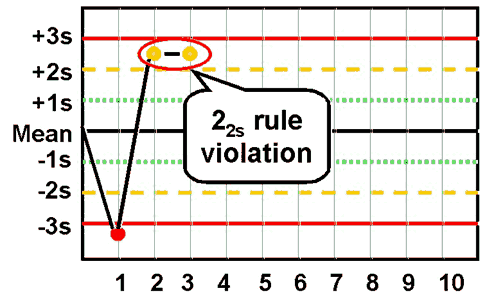
22s - reject when 2 consecutive control measurements exceed the same mean plus 2s or the same mean minus 2s control limit.
|
|
R4s - reject when 1 control measurement in a group exceeds the mean plus 2s and another exceeds the mean minus 2s. Please note: this rule should only be interpreted within-run, not between-run.
|
|
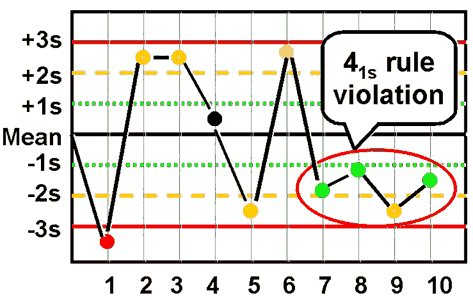
41s - reject when 4 consecutive control measurements exceed the same mean plus 1s or the same mean minus 1s control limit.
|
|
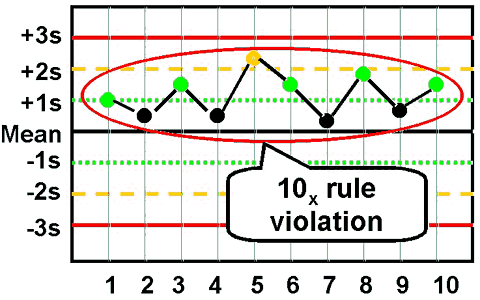
10x - reject when 10 consecutive control measurements fall on one side of the mean.
|
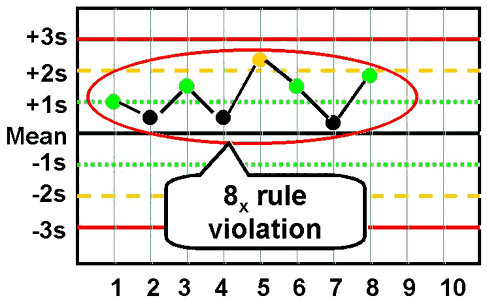
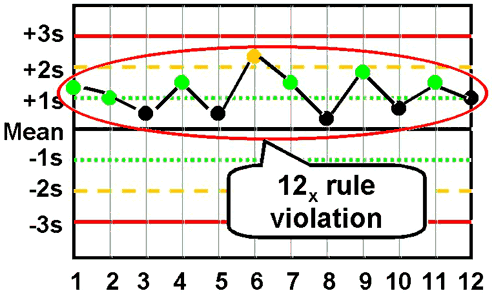
| In addition, you will sometimes see some modifications of this last rule to make it fit more easily with Ns of 4: |
|
8x - reject when 8 consecutive control measurements fall on one side of the mean.
|
|
12x - reject when 12 consecutive control measurements fall on one side of the mean.
|
The preceding control rules are usually used with N's of 2or 4, which means they are appropriate when two different control materials are measured 1 or 2 times per material.
What are other common multirules?
In situations where 3 different control materials are being analyzed, some other control rules fit better and are easier to apply, such as:
|
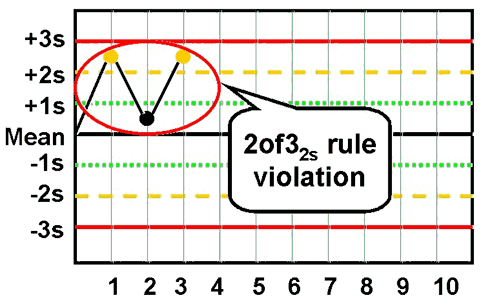
2of32s - reject when 2 out of 3 control measurements exceed the same mean plus 2s or mean minus 2s control limit;
|
|
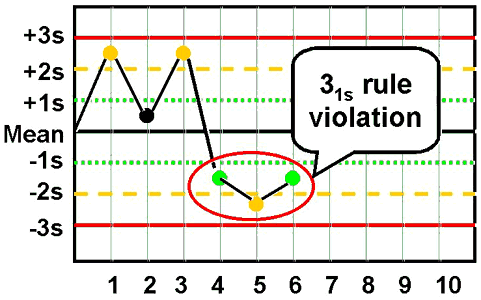
31s - reject when 3 consecutive control measurements exceed the same mean plus 1s or mean minus 1s control limit.
|
|
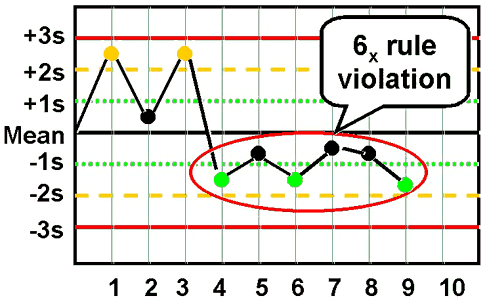
6x - reject when 6 consecutive control measurements fall on one side of the mean. |
| In addition, you will sometimes see some modification of this last rule to include a larger number of control measurements that still fit with an N of 3: |
|
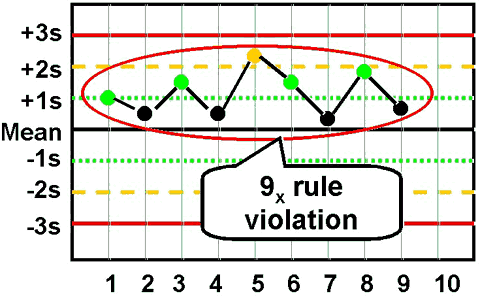
9x - reject when 9 consecutive control measurements fall on one side of the mean. |
| A related control rule that is sometimes used, particularly in Europe, looks for a "trend" where several control measurements in a row are increasing or decreasing [note: it is exceedingly rare to see this rule in use, and obviously it is not ever part of the Westgard Rules]: |
|
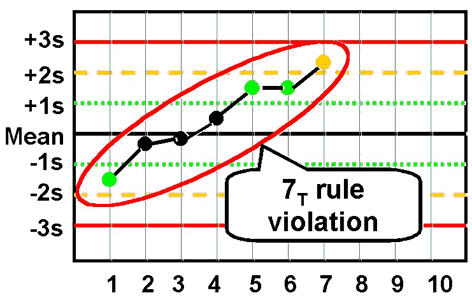
7T - reject when seven control measurements trend in the same direction, i.e., get progressively higher or progressively lower. |
How do you perform multirule QC?
You collect your control measurements in the same way as you would for a regular Levey-Jennings control chart. You establish the means and standard deviations of the control materials in the same way. All that's changed are the control limits and the interpretation of the data, so multirule QC is really not that hard to do! For manual application, draw lines on the Levey-Jennings chart at the mean plus/minus 3s, plus/minus 2s, and plus/minus 1s. See QC - The Levey Jennings chart for more information about preparing control charts.
In manual applications, a 12s rule should be used as a warning to trigger application of the other rules, thus anytime a single measurement exceeds a 2s control limit, you respond by inspecting the control data using the other rules. It's like a yield or warning sign at the intersection of two roads. It doesn't mean stop, it means look carefully before proceeding.
How do you "look carefully"? Use the other control rules to inspect the control points. Stop if a single point exceeds a 3s limit. Stop if two points in a row exceed the same 2s limit. Stop if one point in the group exceeds a plus 2s limit and another exceeds a minus 2s limit. Because N must be at least 2 to satisfy US CLIA QC requirements, all these rules can be applied within a run. Often the 41s and 10x must be used across runs in order to get the number of control measurements needed to apply the rules. A 41s violation occurs whenever 4 consecutive points exceed the same 1s limit. These 4 may be from one control material or they may also be the last 2 points from a high level control material and the last 2 points from a normal level control material, thus the rule may also be applied across materials. The 10x rule usually has to be applied across runs and often across materials.
Computer applications don't need to use the 12swarning rule. You should be able to select the individual rejection rules on a test-by-test basis to optimize the performance of the QC procedure on the basis of the precision and accuracy observed for each analytical method and the quality required by the test.
What is N?
When N is 2, that can mean 2 measurements on one control material or 1 measurement on each of two different control materials. When N is 3, the application would generally involved 1 measurement on each of three different control materials. When N is 4, that could mean 2 measurements on each of two different control materials, or 4 measurements on one material, or 1 measurement on each of four materials.
In general, N represents the total number of control measurements that are available at the time a decision on control status is to be made.
Why use a multirule QC procedure?
Multirule QC procedures are obviously more complicated than single rule procedures, so that's a disadvantage. However, they often provide better performance than the commonly used 12s and 13s single-rule QC procedures. There is a false-alarm problem with a 12s rule, such as the Levey-Jennings chart with 2s control limits; when N=2, it is expected than 9% of good runs will be falsely rejected; with N=3, it is even higher,about 14%; with N=4, it's almost 18%. That means almost 10-20%of good runs will be thrown away, which wastes a lot of time and effort in the laboratory. While a Levey-Jennings chart with 3s control limits has a very low false rejection rate, only 1% or so with Ns of 2-4, the error detection (true alarms) will also be lower, thus the problem with the 13s control rule is that medically important errors may not be detected. (See QC - The Rejection Characteristics for more information about the probabilities for error detection and false rejection.)
The advantages of multirule QC procedures are that false rejections can be kept low while at the same time maintaining high error detection. This is done by selecting individual rules that have very low levels of false rejection, then building up the error detection by using these rules together. It's like running two liver function tests and diagnosing a problem if either one of them is positive. A multirule QC procedure uses two or more statistical tests (control rules) to evaluate the QC data, then rejects a run if any one of these statistical tests is positive.
Are there similiar strategies for QC testing and diagnostic testing?
Yes, a QC test is like a diagnostic test! The QC test attempts to identify problems with the normal operation of an analytical testing process, whereas the diagnostic test attempts to identify problems with the normal operation of a person. Appropriate action or treatment depends on correctly identifying the problem.
Both the QC test and the diagnostic test are affected by the normal variation that is expected when there are no problems,i.e., the QC test attempts to identify changes occurring beyond those normally expected due to the imprecision of the method, whereas the diagnostic test attempts to identify changes beyond those normally expected due to the variation of a population (the reference range or reference interval for the test) or the variation of an individual (intra-individual biological variation). The presence of this background variation or "noise" limits the performance of both the QC test and the diagnostic test.
Are there similar performance characteristics for QC and diagnostic tests?
This background variation causes false alarms that waste time and effort. These false alarms are more properly called false positives for a diagnostic test and false rejections for a QC test, but both are related to a general characteristic called "test specificity." True alarms are called true positives for a diagnostic test and are referred to as error detection for a QC test, and both are related to a general characteristic called "test sensitivity." Sensitivity and specificity, therefore, are general performance characteristics that can be applied to a test that classifies results as positive or negative (as for a diagnostic test) or accept or reject (for a QC test).
Diagnostic tests are seldom perfectly sensitive and perfectly specific! Therefore, physicians have developed approaches and strategies to improve the performance of diagnostic tests. One approach is to adjust the cutoff limit or decision level for classifying a test result as positive or negative. Both sensitivity and specificity change as this limit changes and improvements in sensitivity usually come with a loss of specificity, and vice versa.
QC procedures, likewise, seldom perform with perfect error detection and no false rejections. Laboratories can employ similar approaches for optimizing QC performance. Changing the control limit is like changing the cutoff limit, and improvements in sensitivity usually come at a cost in specificity (the 12s rule is an example). Wider control limits, such as 2.5s, 3s, and 3.5s lead to lower error detection and lower false rejections.
How do you use multiple tests to optimize performance?
Another approach for optimizing diagnostic performance is to use multiple tests. To improve sensitivity, two or more tests are used together and a problem is identified if any one of the tests is positive - this is parallel testing. To improve specificity, a positive finding from a sensitive screening test can be followed up with a second more specific test to confirm the problem - this is serial testing. Both sensitivity and specificity can be optimized by a multiple testing approach, but again these changes usually affect both characteristics.
Strategies with multiple tests can also be used to optimize the performance of a QC procedure. Multirule QC is the general approach for doing this. The objectives are to reduce the problems with the false alarms or false rejections that are caused by the use of 2s control limits, while at the same time improving error detection over that available when using 3s control limit. The multiple tests are different statistical tests or different statistical control rules, and the strategies are based on serial and parallel testing.
- False alarms are minimized by using the 12s rule as a warning rule, then confirming any problems by application of more specific rules that have a low probability of false rejection (serial testing).
- True alarms or error detection are maximized by selecting a combination of the rules most sensitive to detection of random and systematic errors, then rejecting a run if any one of these rules is violated (parallel testing).
When should you use a multirule QC procedure?
Not always! Sometimes a single rule QC procedure gives you all the error detection needed while at the same time maintaining low false rejections. This generally means eliminating the 12s rule because of its high false rejections and considering others such as 12.5s, 13s, and 13.5s which have acceptably low false rejection rates. The remaining issue is whether adequate error detection can be provided by these other single rule QC procedures. If medically important errorscan be detected 90% of the time (i.e., probability of error detection of 0.90 or greater), then a single rule QC procedure is adequate. If 90% error detection can not be provided by a single rule QC procedure, then a multirule QC procedure should be considered. In general, you will find that single rule QC procedures are adequate for your highly automated and very precise chemistry and hematology analyzers, but you should avoid using 2s control limits or the 12s control rule to minimize waste and reduce costs. Earlier generation automated systems and manual methods will often benefit from the improved error detection of multirule QC procedures.
To figure out exactly when to use single rule or multirule QC procedures, you will need to define the quality required for each test, look at the precision and accuracy being achieved by your method, then assess the probabilities for false rejection (Pfr) and error detection (Ped) of the different candidate QC procedures. Aim for 90% error detection (Ped of 0.90 or greater) and 5% or less false rejections (Pfr of 0.05 or less). With very stable analytical systems that seldom have problems, you may be able to settle for lower error detection,say 50%. (See QC - The Planning Process for practical approaches to select appropriate single rule and multirule QC procedures.)
For more information, see these references:
- Westgard JO, Barry PL, Hunt MR, Groth T. A multi-rule Shewhart chart for quality control in clinical chemistry. Clin Chem 1981;27:493-501.
- Westgard JO, Barry PL. Improving Quality Control by use of Multirule Control Procedures. Chapter 4 in Cost-Effective Quality Control: Managing the quality and productivity of analytical processes. AACC Press, Washington, DC, 1986, pp.92-117.
- Westgard JO, Klee GG. Quality Management. Chapter 16 in Fundamentals of Clinical Chemistry, 4th edition. Burtis C, ed., WB Saunders Company, Philadelphia, 1996, pp.211-223.
- Westgard JO, Klee GG. Quality Management. Chapter 17 in Textbook of Clinical Chemistry, 2nd edition. Burtis C, ed., WB Saunders Company, Philadelphia, 1994, pp.548-592.
- Cembrowski GS, Sullivan AM. Quality Control and Statistics, Chapter 4 in Clinical Chemistry: Principles, Procedures, Correlations, 3rd edition. Bishop ML, ed., Lippincott, Philadelphia, 1996, pp.61-96.
- Cembrowski GS, Carey RN. Quality Control Procedures. Chapter 4 in Laboratory Quality Management. ASCP Press, Chicago 1989, pp.59-79.