Basic QC Practices

An introduction to the theory and concepts of quality control in the healthcare laboratory. Dr. Westgard also gives a preview of the articles that follow in this critical series on Basic QC Practices.

• Need for QC?
• A simple graphical tool - the QC chart
• In the beginning, there was Shewhart
• Learning the QC lingo?
• Doing the deed
• References

Please note: an updated version of this lesson is available in the Basic QC Practices, Third Edition.

Need for QC

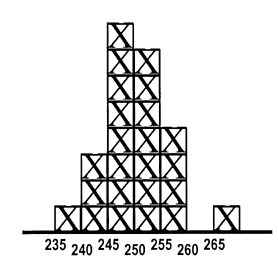The product of a testing process is a numerical result. Unlike a physical product that can be inspected to assess whether it looks good or bad, you can't look at a test result and tell whether it's valid. 247 - what do you think? If this is a patient sample, do you think the test result is of good quality (meaning the correct value)?

If the value of 247 is measured on a sample that has been analyzed before and has the values shown in the accompanying histogram, do you think the test result is of good quality? Because values between 240 and 260 have often been observed in past measurements, it is expected that this new value should also fall in that range if everything is working okay, therefore, the patient test results included in this run of measurements are also most likely correct.

A simple graphical tool - the QC chart

Click here to see an animation about the QC chart.

In the laboratory, control charts are used to make it simple to compare today's observed value with what is 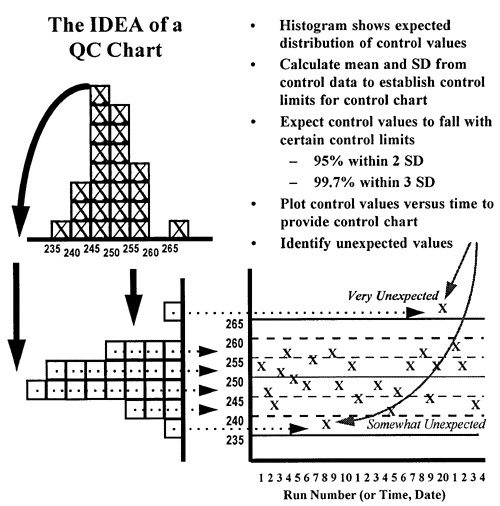expected based on past history. As shown in the second figure, by turning the histogram sideways and spreading the results out according to the time they were collected, it is easy to see how each observation compares to the expected distribution of past observations, which are shown by the central line and certain limits calculated from the mean and standard deviation (SD) of the of the past control data. In this figure, the limit lines correspond to the mean plus/minus 1 SD, 2 SD, and 3 SD. Assuming a gaussian or normal distribution, it would be expected that about 68% of the points fall within 1 SD of the mean, 95% within 2 SD of the mean and 99.7% within 3 SD of the mean. Therefore, it would be very unexpected (0.3% chance) to observe a control value greater than 3 SD from the mean and such an observation usually indicates there is a problem with the method. It is somewhat unexpected to observe a control value greater than 2 SD from the mean, but this will happen at least 5% of the time when analyzing 1 control per run, so it may indicate a real problem or it may be a false alarm. It is very common (32% chance) to see individual values beyond 1 SD from the mean, therefore this control limit is of no value for making a judgment about method performance based on a single control value.

That's the idea behind statistical quality control. See if you can get the right answer for a known sample. The right answer is actually a range of values that are calculated from the mean and standard deviation of past results. That mean and control limits can be shown on a control chart to make it simple to plot new control measurements and see how they compare with the expected range of values.

In the beginning, there was Shewhart

Walter A. Shewhart was a statistician at Bell Telephone Laboratories who developed the scientific basis for statistical process control. Shewhart stated that "the object of industry is to set up economic ways of satisfying human wants and in so doing to reduce everything possible to routines requiring a minimum amount of human effort. Through the use of the scientific method, extended to take account of modern statistical concepts, it has been found possible to set up limits within which the results of routine efforts must lie if they are to be economical. Deviations in the results of a routine process outside such limits indicate that the routine has broken down and will no longer be economical until the cause of trouble is removed." Shewhart made this statement in the preface to his book on the "Economic Control of Quality of Manafactured Product" that was published in 1931.

Statistical process control, from the beginning, has been concerned with achieving the desired quality (satisfying human wants) at minimum cost (economic control). Shewhart identified critical elements such as the expected variation of a routine process, a way to set limits that will identify when the routine has broken down, and the need to eliminate causes of trouble when the process was observed to exceed those limits.

Almost twenty years passed before Levey and Jennings introduced statistical control methods in clinical laboratories in 1950 [2]. Shewhart's original recommendations called for making a group of measurements, calculating the average and range (maximum difference), then plotting the average and the range on two different control charts. Levey and Jennings proposed making duplicate measurements on a patient specimen. Because the actual level of the measured constitutent varied from specimen to specimen, this was a more difficult application. Henry and Segalove [3] developed an alternative procedure in which a stable reference sample was analyzed repeatedly and individual measurements were plotted directly on a control chart. This reference sample type of QC in which individual values or single values are plotted directly is commonly known today as a Levey-Jennings chart.

Since that time, industry has developed stable control products that mimic patient samples, thus today there are safe QC materials readily available for most established tests. A better understanding of the performance characteristics of QC procedures has been developed [4], which has led to refinements such as the multirule procedure for evaluating and interpreting control data [5]. Strategies for cost-effective operation have been further refined [6]. Computer programs have been developed to implement statistical control procedures by performing the necessary calculations, preparing graphical displays, applying the desired control rules, and alerting analysts to problem situations. Today, support for handling control results is provided by most automated analyzers, information systems, and even point-of-care devices.

Learning the QC lingo

Statistical process control is the general term used to describe those aspects of a control system in which statistics are applied to determine whether observed performance is within the expected variation of the process, in contrast to other components of a total control system such as preventive maintainence, instrument function checks, operator training, etc., that are included in CLIA's broad definition of quality control.

Statistical control procedure is used here to refer to a specific protocol for analyzing a specific number of control materials and interpreting a specific number of test results. In healthcare laboratories, a control procedure is usually implemented by collecting test results on stable control materials, then plotting those control observations on a control chart that has specified control limits, or by evaluating those control results by data calculations employing specified decision criteria or control rules.

Control chart is a graphical method for displaying control results and evaluating whether a measurement procedure is in-control or out-of-control. Control results are plotted versus time or sequential run number; lines are generally drawn from point to point to accent any trends, systematic shifts, and random excursions.

Control limits are lines drawn on a control chart to provide graphical criteria for assessing whether a measurement procedure is in-control or out-of-control. These control limits are usually calculated from the mean and standard deviation (SD, or s) determined for a given control material. Typically the interpretation is based on a specified number of results or points exceeding a certain control limit when in-control patient test results are reported. When out-of-control, the run is rejected and no test results can be reported.

Control rule means a decision criterion for judging whether an analytical run is in-control or out-of-control. It is commonly defined by a symbol of the form A_L, where A is an abbreviation for a statistic or represents a number of control measurements, and L identifies the control limits, often specified as the mean plus or minus a multiple of the standard deviation (s) or sometimes by a specified probability for false rejection (P_fr). Some examples follow:

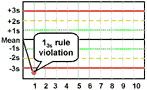1_3s refers to a control rule that is commonly used with a Levey-Jennings chart when the control limits are set as the mean plus 3s and the mean minus 3s. A run is rejected when a single control measurement exceeds the mean plus 3s or the mean minus 3s control limit.

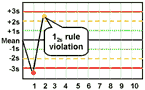1_2s refers to the control rule that is commonly used with a Levey-Jennings chart when the control limits are set as the mean plus/minus 2s. In the original Westgard multirule QC procedure, this rule is used as a warning rule to trigger careful inspection of the control data by the following rejection rules.

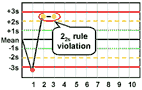
2_2s - reject when 2 consecutive control measurements exceed the same mean plus 2s or the same mean minus 2s control limit.

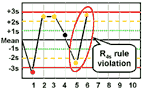
R_4s - reject when 1 control measurement in a group exceeds the mean plus 2s and another exceeds the mean minus 2s.

Run, analytical run, or run length refer to the interval, which could be a period of time or group of samples, for which a decision on control status is to be made. CLIA defines a maximum run length of 24 hours for chemistry analytes and 8 hours for hematology tests. Many laboratories define a shorter period based on changes that may affect the performance of the testing process, such as changing operators, changing reagents, recalibration, or other factors that may make the process susceptible to problems. Run length varies from system to system and laboratory to laboratory. For random access automated systems, a run is usually defined as the time interval at which controls are reanalyzed. For manual systems and batch instruments, a run is often defined as a group (or batch) of samples that are all analyzed at the same time.

Doing the deed

The idea is simple, but the application can be complicated.

First, you need to obtain control materials that are appropriate for the tests of interest and the methods in use. See QC - the Materials for a discussion of important factors, such as matrix effects, stability, vial to vial variation, assayed versus unassayed materials, analyte levels, and pre-treatment problems.

Then you must assay the selected control materials under routine operating conditions to characterize the expected measurement variation and establish the expected distribution of values. This usually involves obtaining at least 20 values and calculating the mean and standard deviation. There are a number of pitfalls from using bottle values or other estimates of the means, standard deviations, and control limits, so you need to be careful with this step. See QC - the Calculations for more information about data calculations.

Next you need to define appropriate control rules, numbers of control measurements (N), and the analytical run length. See QC - the Regulations for the legal requirements for laboratory QC. See QC - the Planning Process for a brief description of QC planning and links to other materials on this website.

You must also define how you will implement these rules and Ns - manual plotting, or computer assessment by the analyzer, a PC workstation, or a laboratory information system. For manual implementation, see QC - the Levey-Jennings Control Chart for directions on how to prepare the control chart, plot control results, and interpret control data.

Finally, you should prepare written guidelines to define the QC procedure in detail. This written document is important for teaching laboratory analysts the QC procedure and establishing a uniform practice. It is also necessary for meeting US regulatory requirements.

Now you're ready to implement QC. See QC - the Practice for a summary and review of the whole approach. See FAQs about QC for additional information about some of the nitty- gritty problems and issues with routine QC.

References

1. Shewhart WA. Economic Control of Quality of Manufactured Product. New York; D. Van Hostrand Company, Inc., 1931.
2. Levey S, Jennings ER. The use of control charts in the clinical laboratory. Am J Clin Pathol 1950;20:1059-66.
3. Henry RJ, Segalove M. The running of standards in clinical chemistry and the use of the control chart. J Clin Pathol 1952;27:493-501.
4. Westgard JO, Groth T, Aronsson T, Falk H, deVerdier C-H. Performance characteristics of rules for internal quality control: probabilities for false rejection and error detection. Clin Chem 1977;23:1857-67.
5. Westgard JO, Barry PL, Hunt MR, Groth T. A multi-rule Shewhart chart for quality control in clinical chemistry. Clin Chem 1981;27:493-501.
6. Westgard JO, Barry PL. Cost-Effective Quality Control: Managing the Quality and Productivity of Analytical Processes. Washington, DC:AACC Press, 1986.