Guest Essay
QC-Dependent Risk Reduction
Hassan Bayat of Sina Lab in Iran contributes additional discussion points to the Clinical Chemistry Journal Club coverage of the Woodworth et al study of HbA1c methods.
QC-dependent Risk Reduction: Clinical Chemistry Journal Club Comments
Hassan Bayat, CLS, Sina Lab (Qaemshahr)
January 2015
The 2014 August issue of Clinical Chemistry has a valuable study on the performance of 8 HbA1c methods performed by Woodworth et al(1):
Utilization of Assay Performance Characteristics to Estimate Hemoglobin A1c Result Reliability. Woodworth A, Korpi-Steiner N, Miller JJ, Rao LV, Yundt-Pacecho YP, Kuchipudi L, Parvin CA, Rhea JM, Molinaro R, Clin Chem 2014;60(8):1073-1079.
Woodworth et al. in their remarkable method validation study via using "forty NGSP secondary reference laboratory (SRL) target value–assigned samples (Dr. Randie Little, University of Missouri, performed testing and provided samples for this study for a fee; NGSP SRL)" have done a comparison study using the protocol instructed in the CLSI EP9-A2 document, and also they have determined precision at two levels (around 5 %HbA1c and 10 %HbA1c ) for each assay using the CLSI EP5-A2 protocol.
Recently J. O. Westgard and Sten Westgard in two separate articles have addressed different aspects of this study and commented valuable points about the paper as well as valuable points related to different aspects of QC, method validation, sigma metrics as well as risk assessment (2, 3). Pointing Woodworth et al. study, J. O. Westgard hopes "this will lead to widespread discussions throughout the clinical chemistry community". Here are my comments to add to the discussion.
Establishing Quality comes BEFORE Controlling Quality
Woodworth et al. correctly define the wrong patient results as "unreliable patient results, which are defined as results containing measurement errors that exceed an allowable total error (TEa) specification". But just knowing TEa specification is not sufficient to determine whether performance is acceptable or unacceptable. To judge acceptability, in addition to knowing TEa, we need to know that how many of the results are allowed to be outside of the TEa limits, i.e. allowable defect rate. Given the most utilized formula for calculating total error (TE) as Bias + 1.65CV, we are allowed to produce as much as 5% "unreliable patient results" (note that this formula is the least demanding one!). Using the Risk Assessment language, based on this formula the allowable residual risk is 5%.
Therefore, for acceptable performance, method bias and CV must be so small that the calculated Total Error is less than TEa, i.e. B + 1.65CV < TEa. In the Six Sigma language, this criterion of "B + 1.65CV" less than TEa translates in a Sigma-metric (SM) of greater than 1.65; meaning that a performance achieves minimal acceptability if it has a SM of ≥1.65. If method validation (MV) study for a method reveals that its SM is less than 1.65, such a method should be rejected and shouldn't be used in laboratories at all; and therefore, planning QC for an unacceptable method is unnecessary.
This point is overlooked in the Woodworth et al. study. In the study, SMs of three methods at 6% TEa are less than 1.65 (1.57, 1.43 and 0.36 for Variant II, Tosoh G8 and Integra 800, respectively), meaning that these methods - in the best situation and during their most stable performance - produce more than 5% unreliable patient results. Despite this fact, Woodworth et al. have tried to find an appropriate QC program to control them and concluded that maximum QC (3 levels, 3 times per day) should be performed to achieve the necessary error detection.
Their mistake originates from an assumption that any performance, regardless of its SM, is acceptable. Ignoring whether the observed quality is acceptable or not, they have focused on the determining the QC plan. To do this they have used performance specifications (i.e. bias and CV) determined via Method Validation studies to find QC programs that assures the "observed performance" during Method Validation is stable in the future routine use for testing patient samples. This way, Woodworth et al. have missed the first important application of the MV outcomes: In the first step, data acquired from MV experience must be used to estimate error rate and judge about the acceptance/rejection of the "observed performance".
If the TEa is considered as 5%, which may be the 2015 goal for NGSP and CAP, the SMs of mentioned methods are even worse (0.83, 0.59 and negative). The negative SM of Integra 800 is the result of its bias being greater than TEa. Note that when bias is greater than TEa, the method completely missing the goal and therefore, even when performing completely stable, the method generates more than 50% erroneous results. If we use CVs and regression equation presented for Integra 800 in table 1 of the article, CV and bias at clinically important level of 6.5 %HbA1c are 2.15% and 5.1%, respectively. With such bias, even when the method is in stable performance approximately 52% of the results are more than 5% away from the target; i.e. 52% unreliable results, or a residual risk of 52% (here it seems that we'd better talk of "residual safe"; because the number of safe results are small than the risky ones!). No doubt such a weak performance should be rejected instead of trying to control its "stable" performance.
To conclude, we can't just accept any stable performance! First, performance must produce less than 5% out-of-TEa results to demonstrate quality, and then we can plan appropriate QC to control its quality. Expanding the running advice of J.O. Westgard we have to "do right QC right" for right quality.
Although Woodworth et al. have tried to establish a model to "transition from using QC to monitor instrument failure to using QC to minimize risk and/or mitigate residual risk of reporting an inaccurate result", they have overlooked method acceptability, their model ends with QC plans that are "generated to monitor stability of laboratory instruments and methods". (Quite possibly, there is an assumption that applying more stringent QC plans can improve method performance. As discussed in detail below, such an assumption is not right.)
How to determine Bias
Woodworth et al. sent "forty NGSP secondary reference laboratory (SRL) target value–assigned samples to each laboratory" and via using CLSI EP 9-A2 determined correlation coefficient (r2) and linear regression equation for all the methods. All the r2s were greater than 0.975, so based on the EP 9-A2 we can use the linear regression equation to calculate bias at clinically important levels. Despite having in hand all the necessary materials (i.e. an r2 of ≥ 0.975 and the regression equation) for calculating bias, Woodworth instead used the observed vs. assigned values of the controls to calculate bias; expressed under the table 1 in the article as " % Bias = 100 × (observed mean - value)/assigned value".
In the table 1 below I have reversed the calculation used by Woodworth et al. into 'Assigned value = (100 × observed value) / (%Bias + 100)' to estimate the assigned values of the controls. Then, I have calculated bias at assigned value levels using regression equation (via substituting assigned values with "x" in the regression equation), so we can compare biases derived from the two different ways with each other (Table 2. In this table, biases presented in the original article are called "Control derived Bias" and biases calculated using regression equation are called "Regression derived Bias").
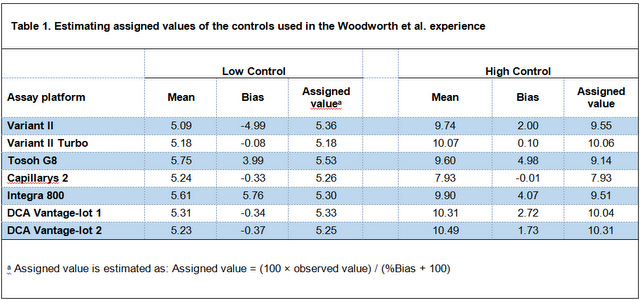
Table 2. Comparing biases derived from two different ways; Using values assigned to control materials vs. using regression equation.
As is emphasized in the EP 9-A2 (and other scientific texts on estimating bias), because of the problems with commercial control materials, especially lack of commutability, the best way to estimate bias between two methods is the comparison study using un-manipulated patient samples. As tale 2 shows, biases calculated from controls by Woodworth et al. around the level of 5 %HbA1c for three methods (Capillarys 2, DCA Vantage-lot 1, and DCA Vantage-lot 2) are very different than the biases calculated from the regression equation (the most difference is with DCA Vantage-lot 2; -0.34 vs. 0.78).
Determining quality at the most clinically important level;
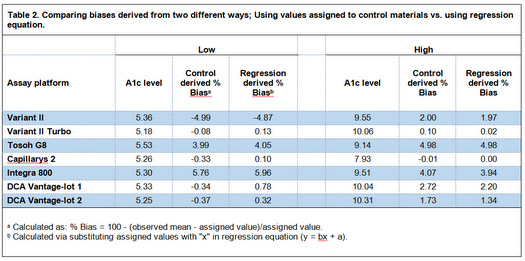
In table 3, I have calculated Sigma-metrics (SM) at 6.5 %HbA1c because "we're probably most interested is the performance at around 6.5% HbA1c, since that is where the diagnosis of diabetes is made"(3). Although J. O. Westgard in his commentary has calculated SMs at this level(2), he averaged CVs of the low and high control materials to estimate CV at 6.5 %HbA1c level. Given that 6.5 is closer to low control level, the better estimate of CV at 6.5 %HbA1c could be determined via interpolating between low and high level CVs. I have used the first order equation for the line connecting the points "low-mean, low-CV" and "high-mean, high-CV" to calculate CV at 6.5 level. The biases at this level for the methods are calculated from respective regression equations determined by Woodworth et al. Then, I have compared the SMs calculated using interpolated CVs with what J. O. Westgard determined.
Although in the table 3 the interpolated CVs are different from average CVs calculated by Westgard, but when the CVs are used to calculate Sigma-metrics, it becomes clear that the Sigma-metrics derived from both ways are approximately the same, and therefore, "for all these cases, there would [be] little if any difference in the interpretation of sigma quality and its implications for risk and QC!"(2). This comparison shows that comparing "Complex solutions vs. simple rules", "in this case, a simple rule to use an average estimate of CV at the medically important decision concentration of 6.5 %Hb may actually provide an equal estimate of risk than the more complicated calculation of an interpolated CV"(2) (The underlined words are the words that I've substituted with the original words; 'a point', 'sigma', 'better', and 'patient-weighted sigma').
Table 3. Comparing CVs and SMs derived from two different ways: Interpolating vs. averaging.
Sigma Metrics: Level-Specific vs. Patient-Weighted
Woodworth et al. introduced a new version of Sigma-metrics called "Patient-weighted σ values". To calculate this index, "a representative patient distribution of Hb A1c values was obtained from 1 facility over a 2-week period. Sigma values [(TEa - %Bias)/CV] for each instrument were calculated at each Hb A1c concentration and averaged over the observed Hb A1c patient distribution to obtain patient-weighted σ values."
For the methods that have different quality at different levels through measuring range, patient-weighted SMs are supposed to relate the different composition of patient results to the predicting the number of erroneous results in the application of those methods.
If we use a same method in two different compositions of patient results, the risk of producing erroneous results would be different. For example, if an A1c method with a quality of 5-sigma at 5 %Hb and a quality of 3-sigma at 7%Hb is used in an screening program for young healthy people, it will do very well and will produce few erroneous results because most of the results will be around 5; where the method is of excellent quality. But when used in monitoring diabetic patients, the people whom A1c levels are around 7, the risk of producing erroneous results will be high because of marginal quality at this level.
This new version of Sigma-metrics has applications in the method selection and also in the long term risk monitoring. In the case of method selection, patient-weighted σ values could be used in establishing buying criteria. Meaning that when a laboratory is evaluating a new testing device/kit for purchase, they can forecast the frequency distribution of the results that they will produce with that device/kit (based on the past experience or other sources), and then, using the methodology explained by Woodworth et al, combine those data with the performance claims made by the manufacturer to determine patient-weighted σ values. This way, they can assess the risk of producing erroneous results. This way, a particular testing method could be appropriate for one setting and inappropriate for the other due to the different patient populations they serve.
The other application of patient-weighted σ values is for continuous quality monitoring. After establishing a method, laboratory can periodically review the frequency distribution of the results, and recalculate the patient-weighted σ value. If the patient-weighted σ value is getting worse - because the frequency distribution is changing so the number of results around low-quality level is increasing - maybe it's the time to rethink this testing method. I'm not saying that without patient-weighted sigma values we are not able to do such risk assessments. No doubt, both the initial assessment for buying a method and continuous assessment for monitoring quality are doable without calculating patient-weighted sigma values. However, using patient-weighted sigma values makes such activities more objective and therefore adds value to the practice.
Despite the mentioned potential benefits, there is an important caveat about misuse of patient-weighted σ values instead "level-specific" sigma values when communicating the reliability of results produced at different levels. For example, suppose we have an A1c method that is of 5.5 sigma quality at 6 %Hb level and of 3 sigma quality at 9 %Hb; and also suppose 95% of the results we produce with this method are around 6 %Hb, and 1% of the results are around 9 %Hb, and the remaining 4% somewhere in-between. With this performance-frequency combination, we will have a patient-weighted sigma value of greater than 5. But, regardless of the excellent patient-weighted sigma value that implies to "overall" low risk performance, and regardless of the large number of high-quality results that are produced around 6 %Hb level, the few results that are produced around 9 %Hb are not reliable. If we communicate to the physician the excellent patient-weighted sigma value for this method, and present him/her several A1c results spanning 5 %Hb through 10 %Hb, he/she will interpret and decide about all the patients with high confidence. But if we (hopefully) inform the physician of the large difference between the levels of quality at different levels of the results, then while he/she again make highly confident decisions about the large amount of results around 6 %Hb, when he/she confronts a 10 %Hb result, he/she won't make radical decisions about changing the patient's treatment (maybe shifting to insulin), and instead reorder the test on a method that is of higher quality at upper levels.
In the era of individualized medicine, it's essential that, as an important part of Risk Analysis, we "disclose" to our clients (physicians) the amount of the residual risk that accompanies any individual result. As an analogous example, if we are driving in a high-standard highway that has just 1 kilometer of its surface damaged, while the "overall" quality of the road is still world-class, we still need to be informed of the location of the damage and also the degree of damage; a practice that is usual in the real world. We frequently get such information while driving; kilometers before the "bad" part of the road, we see "CAUTION" signs to inform us to be careful when driving on the damaged part of the road. In the same way, this approach would be the right one in the health care. If we produce many results at the very low-risk part of the measurement range, but we produce just one result that is high-risk (i.e. where the quality is low), we should set up our own "CAUTION " signs on the patient report to alert and warn physicians to be careful when interpreting that result. Using Risk Assessment language, this is the way we disclosure significant residual risk to our clients.
Another "CAUTION" sign that should be put up before patient-weighted σ values: they should not be used to develop QC plans for methods that achieve significantly different quality at different levels. With such methods, the laboratory may need to use multi-level QC design(4). A multi-level QC is composed of different plans, including lenient and stringent limits, each appropriate for controlling quality at a different level (the lenient QC for high-sigma level, and the stringent QC for the low-sigma level). To determine QC that is appropriate for any specific level, and so compose a multi-level QC plan, we need level-specific sigma values; not patient-weighted sigma values. Again when "individualizing" is indicated, "overall" patient-weighted sigma values are not helpful.
In short, patient-weighted σ value has some benefits, if and only if, it is used appropriately; i.e. in initial risk assessment when deciding about buying a method, and thereafter, in continuous risk assessment to be aware when the patient population distribution has changed to the point that the method must be replaced. But when it comes to "individualizing", whether communicating individualized information about residual risk at different levels, or individualized QCs appropriate for different levels, patient-weighted σ value doesn't work and we need level-specific sigma values.
Via Making QC More Demanding, We Can't Get More from a Weak Method!
It's important to note that QC plans - at best - can help when performance is stable. The more robust the QC strategy, the more its ability to keep performance stable. In no way can a QC strategy, regardless of how stringent it is, compensate for the bad quality of a method. For example, if we purchase a 0.85 sigma method, this means that if there is no shift in the calibration and/or no increase of imprecision at all, this method in its most stable performance produces 40% erroneous results. If there was a magic QC that could keep this method's performance completely stable, then its error rate could be maintained at 40%; and be prevented from becoming worse. But no QC strategy, even the magic ones, can reduce the error rate of this method to even 39%, let alone reducing to <1%!
In the Woodworth et al. study, Roche Integra 800 having a 0.85 sigma (at a TEa of 7%) is one such weak performance (Table 2 on the paper). In its most stable situation, Integra 800 will produce 40% unreliable results. Woodworth et al. states "if the number of HbA1c patient samples tested between QC events was set at 10 instead of 100, the max E(Nuf) [expected number of final unreliable results] when using the Roche Integra 800 would be <1 out of 100", effectively claiming that increasing the frequency of testing QC materials (i.e. employing a tough QC plan) will decrease the error rate of this method from 40% to <1%. Obviously this conclusion is wrong, and they have to revise their model to address the problem. 0.85 is the patient weighted sigma value calculated in the paper. If we consider 0.5 sigma that is the point sigma value at 6.5 %Hb calculated by J.O. Westgard for this method at a TEa of 6%, the situation is even worse, and while the method is completely stable, 62% of the results produced at this clinically important level are wrong!
Certified but of Poor Quality!?
Woodworth et al. study shows that two NGSP certified A1c methods (Tosoh G8 and Integra 800) can't address the intended quality, i.e. producing at least 95% in-TEa results (Given the sigma values of 1.5 and 0.5 at 6.5 %Hb calculated by Westgard for these methods, respectively, these method produce at most 87% and 38% correct results, respectively).
One wonders how it is possible that certified methods are of such low quality. Maybe the problem lies in the "counting methodology" used by NGSP as certifying a method if it produces ≥ 37 results within TEa out of 40 specimens. It seems that such an approach has low statistical power to determine bias. Woodworth et al. study is a robust evidence that NGSP certification methodology certifies some methods with less than 2 sigma values; the performances that shouldn't be used in laboratories at all; and also NGSP certification methodology certifies some weak 2 to 3 sigma methods that although "theoretically" acceptable, but practically must be considered unacceptable because there is no appropriate statistical QC for controlling them.
It seems that it would be better if NGSP replaces its methodology with regression analysis and also increases the required sample number to at least 100 (similar to the CLSI EP 9-A2 document) to have a statistically more powerful tool to assess bias. Also, NGSP should order manufacturers to do reliable long-term imprecision experiments (like the CLSI EP 5-A2 document). Then NGSP can report sigma values and certify methods that have a quality of ≥ 3 sigma.
What's the Point?
The remarkable Woolworth et al. study highlights the combined effect of high-sigma methods and more demanding QC strategies on reducing the risk of reporting erroneous results. Although at present no authority and regulatory organization, including NGSP, is certifying laboratory testing methods based on the sigma values, and although "manufacturers would never put up with sigma scale ratings of commercial diagnostic tests"(7), by using reliable method validation reports of manufacturers or doing the method validations ourselves, we can calculate sigma values for different methods, and then select methods that are of high quality such as 5 sigma or more.
The other important duty for us is to avoid one size QC, and instead to employ scientific QC plans using "Westgard QC rules [that] have been available for many years as a guide for monitoring QC".
References
- Woodworth A, Korpi-Steiner N, Miller JJ, Rao LV, Yundt-Pacheco J, Kuchipudi L, Parvin CA, Rhea JM, Molinaro R. Utilization of assay performance characteristics to estimate Hemoglobin A1c result reliability. Clin Chem 2014;60:1073-1079.
- James O. Westgard, PhD. Risk-Based QC Plans: Clinical Chemistry Journal Club Comments. Westgard Website November 2014 (http://www.westgard.com/risk-plans-hbA1c .htm)
- Sten Westgard. Sigma-metrics of Six HbA1c methods. Westgard Website November 2014 (http://www.westgard.com/six-hbA1c -methods.htm)
- Westgard JO, Westgard SA. Basic QC practices. Madison WI:Westgard QC, Inc. 3rd ed. 2010
- Westgard JO, Westgard SA. Basic Planning for QC. Madison WI:Westgard QC, Inc. 3rd ed. 2010
- CLSI C24A3. Statistical quality control for quantitative measurement procedures. Clinical and Laboratory Standards Institute, Wayne PA, 2006.
- In lab QC, how much room for improvement? An interview with James Westgard, PhD. CAP TODAY Pathology/Laboratory Medicine/Laboratory Management. October 16, 2014 http://www.captodayonline.com
