Quality Requirements and Standards
Good Laboratory Practices for Statistical QC, Part II:
Some practical advice on the proper set up, implementation and use of QC, as well as a discussion of "standard deviations" from Good Laboratory Practice.
QC Limits and Limitations
- Are these good or bad practices?
- Principles and Assumptions of Statistical QC
- Rejection Characteristics
- Good Laboratory Practices
- Common and Standard Deviations from Good Laboratory Practices
- Concluding Comments
- References
December 2006
One of the major issues identified in the recent ASCP teleconference “A How-Should-I Guide to Laboratory Quality Control” was the need for guidelines for setting QC limits. This issue can be divided into two parts, the 1st dealing with the right multiple of standard deviations and the 2nd dealing with the right estimate of the mean and standard deviation. The 1st part involves selecting the right control rules, e.g., 2s or 3s control limits or 12s or 13s control rules for the Levey-Jennings control chart [1-3]. The 2nd part involves the conditions and number of measurements necessary to properly observe and estimate the mean and standard deviation of the measurement procedure or analytical method.
Many laboratories today still use 2s control limits, in spite of the fact that this practice is known to give a high level of false alarms or false rejections. To counter the problem with false alarms, laboratories try to widen the control limits by using different estimates of the method standard deviation, such as manufacturer’s “bottle values,” peer method SDs as observed for a group of laboratories, and sometime some form of a medically significant SD.
Are these good or bad practices?
CLIA Guidance
The 2003 CLIA Final Rule [4] does not prescribe how to set control limits. Instead, it provides guidance for what the laboratory and the QC procedure should achieve:
§493.1245 Standard: Control procedures
(a) For each test system, the laboratory is responsible for having control procedures that monitor the accuracy and precision of the complete analytic process.
(b) The laboratory must establish the number, type, and frequency of testing control materials using, if applicable, the performance specifications verified or established by the laboratory as specified in §493.1253(b)(3).
(c) The control procedure must (1) detect immediate errors that occur due to test system failure, adverse environmental conditions, and operator performance. (2) Monitor over time the accuracy and precision of test performance that may be influenced by changes in test system performance and environmental conditions, and variance in operator performance.
Notice the emphasis on monitoring accuracy and precision of the complete analytic process. This can best be achieved by measuring liquid control materials that are processed in the same manner as real patient samples. Notice that the laboratory should take into account the performance specifications verified or established by the laboratory by method validation experiments (that’s the focus of §493.1253). That again relates to the precision and accuracy observed for the method in your own laboratory. Notice that the objectives of QC are to detect immediate errors and monitor over time the precision and accuracy of the method. Here again the emphasis is on the performance of the individual method in an individual laboratory.
While CLIA doesn’t tell us how to set control limits, it does focus us on the importance of the precision and accuracy of the measurement procedure in our own laboratory. That guidance is critical if a QC procedure is to detect immediate errors and changes or variations in the performance in our own laboratories. The “how and why” can be understood on the basis of the proper operation of a statistical QC procedure.
Principles and Assumptions of Statistical QC
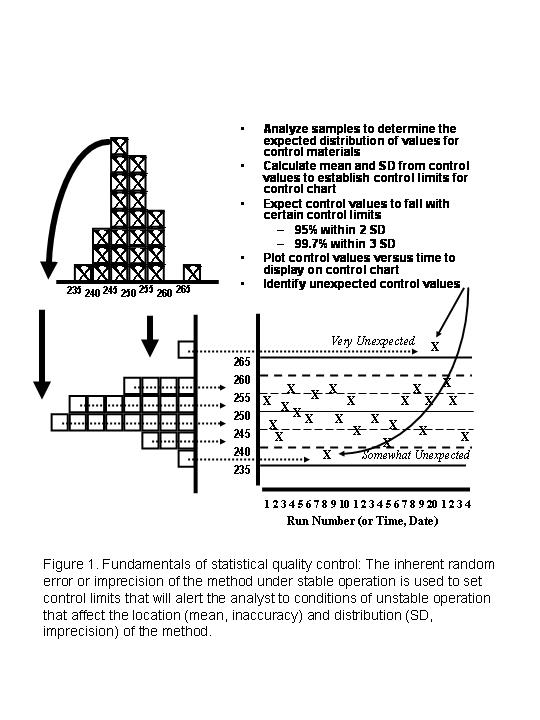 Some of the fundamental principles and assumptions of statistical QC can be understood with reference to Figure 1.
Some of the fundamental principles and assumptions of statistical QC can be understood with reference to Figure 1.
Measurement procedures have an inherent variability, or random error (imprecision, precision), that can be observed by analyzing the same sample again and again. That variability can be estimated from a replication experiment and can be displayed graphically by a histogram. Alternatively, that variability can be displayed point-by-point on a control chart by plotting the value on the y-axis vs time on the y-axis. If that random variability changes, it suggests that something has changed in the measurement procedure. Statistical QC attempts to identify such changes by comparing the currently observed variability with that observed under stable operating conditions. Control limits are drawn on the control chart to help identify conditions where the observed variability no long represents the stable performance observed earlier.
For statistical QC to work in the laboratory, it is assumed that:
- stable specimens are available with aliquots that can be sampled conveniently over a long period of time, which generally requires special materials developed specifically for this purpose, i.e., quality control materials;
- the variability observed is primarily due to the measurement procedure with minimum contributions from the control material itself;
- the distribution of these replicate results is assumed to be “normal” or “Gaussian,” which is reasonable for applications to a measurement procedure; keep in mind, the distribution here is the error distribution of measurements, not the distribution of a healthy or normal patient population (which certainly can not be assumed to be Gaussian).
The range of variation that is expected in routine operation can be predicted from the mean and standard deviation (SD) that are calculated from the replication data.
- 95% of the results are expected to fall between the mean + 2SD and the mean – 2SD: This situation is also described as a 2SD control limit, i.e., a decision criterion where a run is considered out-of-control if 1 result exceeds a 2s control limit, which can also be identified as a 12s control rule.
- 99.7% of the results are expected to fall between the mean +3SD and the mean -3SD, which can also be described as a 3 SD control limit or 13s control rule.
As illustrated in Figure 1, a single point that exceeds a 2 SD control limit is somewhat unlikely occurrence, whereas a single point that exceeds a 3 SD control limit is a very unlikely occurrence. Laboratory analysts know that 1 out of 20 or 5% of control results are expected to exceed 2 SD limits, thus it is common for laboratories to just repeat the control because of the suspicion of a “false rejection.”
The use of 2 SD control limits can be a dangerous practice because it conditions laboratory analysts to expect false alarms, which may then lead them to ignore true alarms. When a control exceeds a 3 SD limit, it is most likely a true alarm because there is such a low probability for false alarms. Ideally, QC procedures should be selected to minimize false alarms and maximize true alarms for medically important errors. It is also critical that control limits be properly established to correctly characterize the variability observed in the individual laboratory, otherwise the QC procedure will not behave as expected.
Rejection characteristics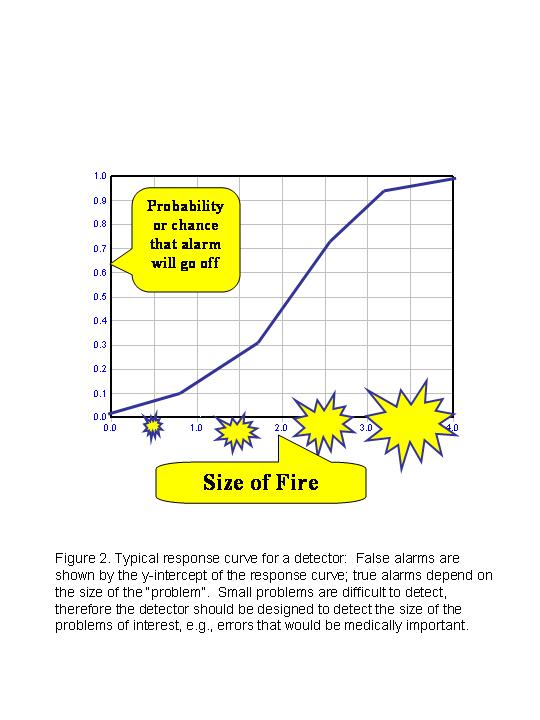
The behavior of different control rules (or limits) can be described by their rejection characteristics, i.e., their probabilities of false rejection and error detection [5].
- Pfr, the probability for false rejection, is the probability of a rejection occurring when there is no error except for the inherent imprecision or random variability of the measurement procedure;
- Ped is the probability for error detection, i.e., the probability of rejection when an error is present in addition to the inherent imprecision or random variability of the measurement procedure.
These characteristics can be understood by analogy with a fire alarm system. You want the false alarms to be low, otherwise the alarm system itself makes us believe there are problems when there really aren’t, causing us to waste time and effort. No alarm system is perfectly sensitive, thus these response curves typically are “s-shaped,” starting out low, becoming steep in the middle, then leveling out at the high end, as shown in Figure 2. You would like the alarm system to be sufficiently sensitive for a problem that is important to detect, but at the same time, NOT generate any false alarms.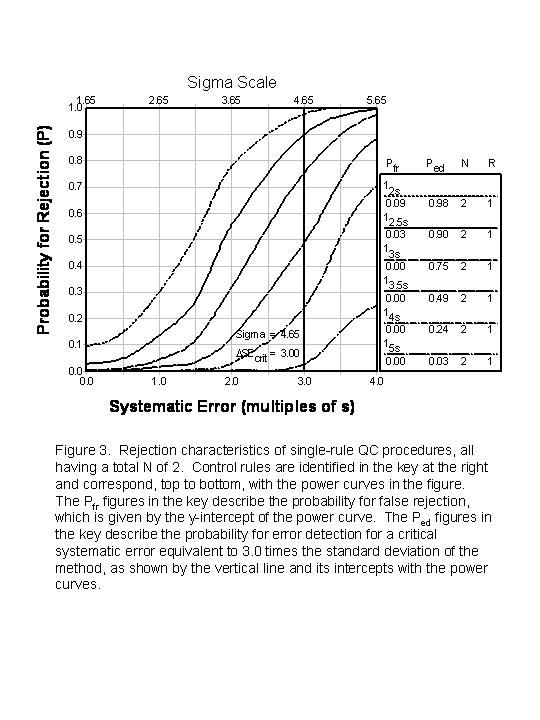 These rejection characteristics for QC procedures are well-known and have been presented in the form of “power function graphs” [6]. These “power curves” show the probability for rejection on the y-axis versus the size of error on the x-axis. Figure 3 is a power function graph for systematic errors. The different curves (top to bottom) correspond to the different lines in the key at the right (top to bottom). Note that all these QC procedures are for N=2, i.e., the total number of control measurements is 2. All these rules are single-rules with control limits varying from 2s (top curve) to 5s (bottom curve).
These rejection characteristics for QC procedures are well-known and have been presented in the form of “power function graphs” [6]. These “power curves” show the probability for rejection on the y-axis versus the size of error on the x-axis. Figure 3 is a power function graph for systematic errors. The different curves (top to bottom) correspond to the different lines in the key at the right (top to bottom). Note that all these QC procedures are for N=2, i.e., the total number of control measurements is 2. All these rules are single-rules with control limits varying from 2s (top curve) to 5s (bottom curve).
To assess Pfr, read the value of the power curve at the y-intercept, e.g., the probability is about 0.10 or a 10% chance of false rejections when 2s control limits are used with N=2. Pfr is about 0.02 or 2.0% for the 12.5s rule and essentially 0.0% for all the rest.
To assess Ped, the size of the error must be specified or calculated. For example, if the size of the systematic error is equivalent to 3 times the standard deviation of the method, as shown by the vertical line on the graph, the probabilities of detecting this error range from 0.98 for the 12s rule to 0.03 for the 15s rule. Typically, the goal for Ped can be set as 0.90, in which case a 12.5s control rule with N=2 will provide ideal behavior with a 0.90 probability for error detection and less than a 0.05 probability for false rejection (actually 0.03).
Good Laboratory Practices
For statistical QC applications to behave according to principles and theory, the control limits must be properly established. This requires that both the mean and standard deviation reflect the behavior of the measurement procedure under the operating conditions in your laboratory. In other words, data from your own laboratory is necessary to characterize the mean and SD, otherwise the behavior of the QC procedure is not predictable.
Select control materials with known stability. In principle, laboratories can prepare their own quality control pools from left-over patient specimens. However, this can be a dangerous practice due to the infectious nature of patient specimens and the unknown stability of frozen patient pools. In practice, it is better and safer to obtain commercially available materials that have been screened for infectious diseases and whose stability has been tested. For chemistry tests, materials are available that typically are stable for 1 to 2 years. For hematology tests, materials are stable for a period of a few months.
There is more detailed guidance from the CLSI document C24-A3 [7]:
C24-A3 6.2 Select Control Materials: The control materials should have characteristics that enable them to provide information about what is going on with the measurement procedure, when performing measurements with the intended patient sample types. A laboratory should obtain enough homogeneous and stable control material to last for at least one year when practical, to minimize the need to perform additional testing and analyze data for establishing baseline statistical characteristics of the measurement procedure with new lots of quality control material. Vial-to-vial variability of the quality control material should be much less than the variation expected for the measurement procedure being monitored, and the QC materials should have demonstrated stability over their claimed shelf life, and over the claimed interval after opening the container, for the analyte of interest. If commercial quality control materials are not available, the laboratory may prepare and aliquot patient pools for this purpose. If this is not practical, the approach to QC recommended in this document is not applicable.
Determine your own mean and SD. The standard practice is to analyze 20 samples of the QC material in your own laboratory to characterize the mean and SD. The general recommendation is to obtain these 20 measurements over a 20 day period. Depending on the nature and stability of the control material itself, this may involve analyzing 20 different bottles of lyophilized material or several different bottles of liquid control material. The higher number of bottles of lyophilized material is needed to account for the variation in the reconstitution and preparation of the material. With liquid control materials, there shouldn’t be as much bottle to bottle variation, so a lower number of bottles may be used.
C24-A3 6.3.1 Imprecision: Imprecision is estimated by repeated measurements on stable control materials during a time interval when the measurement procedure is operating in a stable condition. It is generally accepted than an initial assessment can be made by measuring a minimum of at least 20 different measurements of control material, for each control level, on separate days. If lyophilized control material is utilized, use of 20 different (reconstituted) bottle of control material (over 20 days) is recommended… Higher numbers of control measurements will provide more reliable estimates of imprecision.
C24-A3 6.3.2 Bias: Bias should be evaluated in the context of the application of the measurement results, particularly whether they will be interpreted vs. local norms, reference limits, or cutoffs, or vs. national or international norms. When interpreted vs. local norms, the focus is on the stable performance of the measurement procedure relative to a baseline event, such as a method validation study, a reference range study, a clinical validation study, or a calibration event. In such cases, the bias term is often assumed to be zero and the objective of statistical QC is to monitor changes from that baseline period. When results will be interpreted vs. national or international norms, measurement bias may be estimated…
-
- by comparison with certified values assigned to standard reference materials…,
- comparison of the laboratory’s results with the peer group mean for external quality assessment (proficiency testing) or other interlaboratory comparison programs…,
- comparison of results obtained on a range of patient specimens analyzed by the laboratory’s test method and another routine method…,
- or comparison of results obtained on patient specimens that are analyzed by the test method and a reference method…
Verify your values are within expected or labeled values. It is good practice to utilize assayed control materials that have expected values or expected ranges. Your laboratory mean should be within the range published in the product insert. Interlaboratory means and SDs are relevant because they reflect current testing conditions among laboratories. If the observed means and SDs in your laboratory are not consistent with the product insert values or published interlaboratory statistics, it is very likely that your measurement procedures are not operating under the same conditions as in other laboratories. With highly automated systems, there may be accuracy or bias problems that need to be identified and fixed prior to establishing control limits, often owing to issues with calibration and standardization. For manual methods, differences in precision or random error may be related to analyst skills and techniques, requiring additional systematization of the steps of the process and better training for the analysts.
C24-A3 8.6.2 Assay Control Materials: If assayed control materials are used, the values stated on the assay sheets provided by the manufacturer should be used only as guides in setting the initial control limits for testing new control materials. Actual values for the mean and standard deviation must be established by serial testing in the laboratory. The observed mean should fall within the range published by the manufacturer. EQA and peer-comparison program provide useful measures of the means and SDs observed in other laboratories.
Develop cumulative limits. Obtaining 20 measurements is really a minimum for estimating the standard deviation. It would be better to have about 100 measurements, but that would take too much time to get started. The practical approach is to get 20 measurements initially, then after collecting another 20, calculate the cumulative mean, cumulative SD, and recalculate the control limits, then continue doing this periodic update until the cumulative values reflect approximately 100 measurements.
C24-A3 8.6.5 Cumulative Values: Estimates of the standard deviation (and to a lesser extent the mean) from monthly control data are often subject to considerable variation from month to month, due to an insufficient number of measurements (e.g., with 20 measurements, the estimate of the standard deviation might vary up to 30% from the true standard deviation; even with 100 measurements, the estimate may vary by as much as 10%). More representative estimates can be obtained by calculating cumulative values based on control data from longer periods of time (e.g., combining control data from a consecutive six-month period to provide a cumulative estimate of the standard deviation of the measurement procedure). This cumulative value will provide a more robust representation of the effects of factors such as recalibration, reagent lot change, calibrator lot change, maintenance cycles, and environmental factors including temperature and humidity. Care should be taken to ensure that the method has been stable and the mean is not drifting consistently lower or consistently higher over the six-month periods being combined, for example due to degradation of the calibrator or control materials.
Overlap new lot of controls. When changing to a new lot number of control material, ideally there should be an overlap period while the new material is being analyzed to establish the new control limits. In cases where the overlap period is not sufficient, it is possible to establish the mean value for the new control material in a short time, over say a five-day period, or to start with the manufacturer’s labeled mean value. Then apply the previous estimate of variation (preferably the CV) to establish the control limits. These control limits should be temporary, until sufficient data is collected to provide good estimates of both the mean and SD of the new material.
C24-A3 Establishing the Value of the Mean for a New Lot of QC Material: New lots of a quality control material should be analyzed for each analyte of interest in parallel with the lot of control material in current use. Ideally, a minimum of at least 20 measurements should be made on separate days when the measurement system is known to be stable, based on QC results from existing lots. If the desired 20 data points from 20 days are not available, provisional values may have to be established from data collected over fewer than 20 days. Possible approaches include making no more than four control measurements per day for five different days…
C24-A3 Establishing the Value of the Standard Deviation for a New Lot of QC Material: If there is a history of quality control data from an extended period of stable operation of the measurement procedure, the established estimate of the standard deviation can be used with the new lot of control material, as long as the new lot of material has similar target levels for the analyte of interest as for previous lots. The estimate of the standard deviation should be reevaluated periodically. If there is no history of quality control data, the standard deviation should be estimated, preferably with a minimum of 20 data points from 20 separate days… This initial standard deviation value should be replaced with a more robust estimate when data from a longer period of stable operation becomes available.
Monitor stability of control materials with peer data. When out-of-control problems occur, there may be concerns that the control materials themselves are causing the problems, due to deterioration over time. The best way to separate effects of your method performance from possible effects of the control materials themselves is to find out what’s happening with those control materials in other laboratories. This requires access to peer data obtained on the same lot numbers of control materials. Manufacturers of control materials typically provide this information through Internet peer-comparison surveys.
C24-A3 9 Interlaboratory QC Programs: When laboratories share a common pool (lot number) of control materials and report the results to an interlaboratory program, a database is created that yields statistical information, which may be used to describe or define: (1) intralaboratory and interlaboratory imprecison; (2) individual laboratory bias relative to a peer group; and (3) relationship of analytical and statistical parameters of imprecision and relative bias to medical requirements. For laboratory self-evaluation, peer-related bias and relative imprecision are useful parameters. Participation in an interlaboratory program provides an effe4ctive mechanism to complement external quality assessment (proficiency survey) programs…
Common or Standard Deviations from Recommended QC Practices
In the real world, there are often deviations from these standard practices. If the mean is not properly determined, the control limits will not be centered and counting rules, such 22s, 41s, and 10x, will be improperly triggered, giving rise to false rejections. If the SD is not properly determined, the control limits may be too wide or too narrow. If too wide, the error detection will be lost; if too narrow, false rejections will occur. There are deviant practices that occur so often, they might be considered “standard deviations” from recommended QC practices.
Miscalculation of control limits from out-of-control results. As additional control results are accumulated during routine operation, it is important to flag those results coming from runs that are out-of-control and to eliminate them from any future calculations of mean, SD, and control limits. This does not imply elimination from the QC records, only flagging so they are used in calculations to update the mean, SD, and control limits. Remember that the principle of statistical QC is to characterize the variation expected during stable operation, therefore only data from in-control runs should be included in the calculations. This recommendation conflicts with current practices in laboratories that use 2 SD control limits, where the control ranges will narrow over time if all values outside of 2 SD are eliminated. The right practice here is to eliminate the use of 2 SD control limits, not try to compensate for the problems and limitations that are inherent in the use 2 SD limits.
Misuse of control range from package insert. One common practice is to use the manufacturer’s package insert values to establish control ranges, rather than data from the individual laboratory. Typically this will cause the control limits to be too wide because those values usually reflect the variation observed in several different laboratories. A too large SD will reduce the false rejections (good) but also the error detection (bad). The problem can become severe!
Consider a potassium method that has an SD of 0.05 mmol/L at a level of 5.0 mmol/L, or a 1.0% CV. If a range of 4.75 to 5.25 mmol/L were given by the manufacturer and used by the laboratory, the actual statistical control rule ends of being 15s. The laboratory may think it is using a 12s or 13s rule, but the real statistical rule has much wider limits (0.25/0.05 or 5s). Assuming the same thing happens on two levels of control materials, the power curves in Figure 3 show the effect of the different rules. A 12s rule gives a Ped of 0.98, a 13s rule gives a Ped of 0.75, but a 15s rule provides only a 0.03 probability for detection. You should avoid the 12s procedure because of false rejections, but you want to use 13s rather than 15s to provide better error detection. The problem is that you don’t know which is true for the situation in your laboratory.
Misuse of SD from a peer-comparison group. The group SD is likely to be larger than the SD of an individual laboratory, therefore the control limits will likely be set too wide. Again, this will result in lower false rejections (good) but also lower error detection (bad). To evaluate the effect, take the ratio of the group SD to your within-lab SD and apply the multipler (2 or 3). If the group SD is twice as large as the within-lab SD and you used 2 SD limits, in effect you have implemented a 14s rule (2*ratio SDgroup/SDwithinlab).
Misuse of a target mean from peer-comparison group. This seems like a reasonable practice, but it can cause some interesting problems. Let’s assume implementation of a 13s rule, where the laboratory mean is actually 1 SD higher than the target mean observed for the group. In effect, the control rule on the high side is actually a 12s rule, whereas the control rule operating on the low side is a 14s rule. There will be a much higher chance to detecting errors in the high direction than those in the low direction. There will also be a higher level of false rejections than expected, 2.5% vs 0.0%. There will be additional problems when using multirule procedures. Well over half of the points will be below the target mean, which will cause the 10x rule to be violated. The 22s rule actually becomes 23s on the high side, which lowers error detection, and 21s on the low side, which increases false rejection. The 41s rule becomes 42s on the high side, which lowers error detection, and 4x on the low side, which increases false rejections. This can provide no end of confusion, misunderstanding, and mismanagement of quality.
While it is okay to utilize a target mean when there is insufficient data from your own laboratory, it is critical to get your own data and switch over to your own mean as soon as possible. If the difference between your mean and the target mean from the group is large enough to be worrisome, then investigate the method and validate that it is accurate as operated in your laboratory. This validation may make use of other traceable standard materials, comparison of patient results with a reference quality method, and interference and recovery studies to pinpoint specific analytical problems.
Misuse of clinical or medical control limits. This one sounds good in theory, but is generally bad in practice. There have been some recommendations in the literature to set the control limits on the basis of clinically important changes [8], i.e., some kind of a clinical SD, rather than for statistically important changes, i.e., using the method SD. It is generally believed that the clinical SD will be larger than the statistical SD, therefore the clinical control limits will be wider than the statistical control limits. The reasoning is that a run may be out-of-control based on statistical limits, but still be okay based on clinical limits. The problem is that any control limit, however drawn, still defines a statistical control rule. To understand the true performance, you need to identify the statistical rule and assess the error detection from its power curve.
Let’s take a potassium example again. CLIA sets a quality requirement of 0.5 mmol/L as acceptable performance for a potassium test. If our method has an actual SD of 0.10 mmol/L, a clinical control limit of 0.5 mmol/L would be equivalent to a 15s rule. A systematic error of 0.5 mmol/L amounts to a 5s shift, which is somewhat off-scale on our power function graph in Figure 4. Nonetheless, you can predict that a 13s rule with N=1 would provide better than 90% detection if a 5s shift, whereas a 15s rule with N=1 will provide much less than ideal detection. The right way to address a requirement for quality is in the QC planning process [9, 10], not by a supposedly clinical control limit directly on the control chart. See www.westgard.com/essay8.htm for a more complete discussion of the problems with medical control limits.
Concluding comments
Quality practices for statistical QC mean doing the right QC right!
- The first right applies to selecting appropriate control rules and the appropriate number of control measurements to detect medically important errors, while minimizing false rejections. This was discussed in part 1 of this series and more detailed information is available in the scientific literature [9].
- The second right applies to implementing statistical QC properly, particularly establishing control limits correctly, as described in detail in this discussion and in the CLSI C24-A3 guideline [7].
Statistical QC is a powerful technique for managing the analytical quality of laboratory testing processes, but it must be implemented properly to provide the potential benefits. These benefits include the assurance or guarantee that analytical test results are correct for patient care and that such assurance is provided at the lowest possible cost.
References
- Levey S, Jennings ER. The use of control charts in the clinical laboratory. Am J Clin Pathol 1950;20:1059-66.
- Shewhart WA. Economic Control of Quality of the Manufactured Product. New York:Van Nostrand, 1931.
- Henry RJ, Segalove M. The running of standards in clinical chemistry and the use of the control chart. J Clin Pathol 1952;5:305-11.
- US Centers for Medicare & Medicaid Services (CMS). Medicare, Medicaid, and CLIA Programs: Laboratory Requirements Relating to Quality Systems and Certain Personnel Qualifications. Final Rule. Fed Regist Jan 24 2003;16:3640-3714.
- Westgard JO, Groth T, Aronsson T, Falk H, deVerdier C-H. Performance characteristics of rules for internal quality control: probabilities for false rejection and error detection. Clin Chem 1977;23:1857-67.
- Westgard JO, Barry PL. Cost-Effective Quality Control: Managing the quality and productivity of analytical processes. Washington DC:AACC Press, 1986.
- CLSI C24-A3. Statistical Quality Control for Quantitative Measurement Procedures: Principles and Definitions; Approved Guideline – Third Edition. Clinical Laboratory Standards Institute, Wayne, PA 2006.
- Tetrault GA, Steindel SJ. Daily quality control exception practices, data analysis and critique. Q-Probes. Northfield, IL: College of American Pathologists, 1994.
- Westgard JO. Internal quality control: Planning and implementation strategies. Ann Clin Biochem 2003;40:593-611.
- Westgard JO. Clinical quality vs analytical performance: What are the right targets and target values? Accred Qual Assur 2004;10:10-14.
