Z-Stats / Basic Statistics
Z-3: An Organizer Of Statistical Terms (Part II)
Dr. Madelon F. Zady, Ph.D., talks about the nature of a relationship (correlation) and the strength of a relationship (regression). These are statistical relationships, of course. For other forms of relationship advice, we suggest you consult the webmaster or another website entirely.
EdD Assistant Professor
Clinical Laboratory Science Program University of Louisville
Louisville, Kentucky
May 1999
- A quick review of lesson 2
- Correlation - the strength of a relationship
- Regression - the nature of a relationship
- Correlation vs regression
- Summary
- About the Author
[Lessons 2 and 3 provide a somewhat over-simplified description of the rest of this series. This is done to aid the learner in learning statistical terms and concepts. The lessons are designed to serve as an "organizer" for the coming material. If you are familiar with these statistical terms and concepts, you can quickly review this lesson and lesson 3 and get ready for more detailed materials in Lesson 4 (coming soon).]
A quick review of lesson 2
 Lesson 2 introduced the "organizer" shown here. The first terms - mean and standard deviation - are familiar to laboratorians, particularly the use of the mean +/- 2SD as control limits for statistical quality control (please note, however, that these may not be the best control limits to use). Through familiarity with the Levey-Jennings chart, most laboratorians also recognize that these +/- 2SD limits or 'gates' encompass 95% of the area under a normal or gaussian curve. That area also represents a 0.95 probability, leaving the last 5% of the area, or 0.05 probably, for the outer tails of the normal curve.
Lesson 2 introduced the "organizer" shown here. The first terms - mean and standard deviation - are familiar to laboratorians, particularly the use of the mean +/- 2SD as control limits for statistical quality control (please note, however, that these may not be the best control limits to use). Through familiarity with the Levey-Jennings chart, most laboratorians also recognize that these +/- 2SD limits or 'gates' encompass 95% of the area under a normal or gaussian curve. That area also represents a 0.95 probability, leaving the last 5% of the area, or 0.05 probably, for the outer tails of the normal curve.
Laboratorians have often used +/- 2SD like a standard score. The most common standard score is the z-score, which is the difference between the observed value minus the mean divided by the SD. The z-value of +2 to -2 correspond to the 95% area under the curve, or a 0.95 probability. A value found inside that +/- 2 has a 0.95 probability of being "the same" as the mean value for the distribution.
To use a z-distribution, the true mean (mu) and the true standard deviation (sigma) of a population must be known. Oftentimes these are not available, therefore, it is useful to consider a t-distribution that has a large enough N to approximate a normal distribution. The t-value is interpreted the same way as a z-score. The "gates" of +/- 2t enclose 95% of the area under the t-distribution. A t-test can be used in a comparison of methods experiment to test two means to see if they are "the same," in which case there is no evidence of systematic error between the methods or analyzers.
What if we wanted to test the similarity in results on three different analyzers? There is a problem with doing multiple t-tests, therefore it is a better test to use the F-statistic. Here's where the calculations change and we "drop the square root". Because of the square root, F=t2 (and F1/2=t), therefore the "gates used on the F-distribution will have different numbers such that "+/- 4F" contains 95% of the area. A value that falls into this interval has a 0.95 probability (p=0.95) of being "the same" as the mean of the distribution. A value that falls out of these gates only has a 0.05 probability (p=0.05) or less of being "the same" as the mean of the distribution, therefore we often conclude that such a value is different or "statistically significant."
Correlation - the strength of a relationship
Now we turn to other statistics that describe relationships. The seventh topic in "organizer" is correlation. Correlation is a way to say something about a relationship (and not much more). The mathematics needed for correlation are important mainly because of the way these formulae relate to a more powerful statistics on regression. We will look at the formulae for correlation in a future lesson, however, don't worry too much about the equations because we can use available statistical programs to perform these calculations. The correlation coefficient is set up on an r-scale that ranges from +1.00 to -1.00. A +1.00 means a perfect positive relationship, i.e., as A increases, B always increases. A -1.00 means a perfect inverse relationship, i.e., as A increases, B always decreases. A correlation coefficient close to 0.00 means there is no relationship at all between A and B, i.e., the points will just scatter randomly.
Correlation calculations are commonly performed for data from a comparison of methods experiment, where a series of samples are analyzed by two different methods or instruments. If the correlation results are close to +1.00, then the methods could be considered comparable. The problem with correlation is that it is not very powerful or informative. The range of the data and the number of measurements both affect the observed correlation. In fact, the size of N has a great effect on all the statistics covered so far.
Regression - the nature of the relationship
The last term in the organizer is regression. Regression is a statistical procedure designed to show a linear relationship between two (or even more) variables. The procedure is based upon the mathematical equation for a straight line, which is covered in beginning algebra classes: y = mx + b or y = bx + a. Note that both sets of symbols will be encountered in the literature, therefore you need to recognize which ones are being used. Also, the order of the terms may be presented differently, e.g., y = a + bx (which is how they appear in the method validation lessons on this website).
Like correlation, regression can be used to show a relationship between the x and y variables, as well as to predict the y-values that correspond to critical x-values. For example, in a comparison of methods experiment, where it is of interest to know about the systematic error between methods, the systematic error can be estimated from difference between the calculated y-value and the x-value that represents a critical medical decision level. In a subsequent lesson, this formula will be manipulated in order to demonstrate the many strengths of procedure regression.
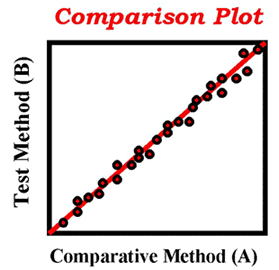 In the y = a + bx equation, a is called the y-intercept and b is called the slope. A perfect relationship between y and x will have an intercept of zero and a slope of one. The graph of this relationship is very familiar and shows a straight line making a 45-degree angle with the base of the graph and passing through the zero point (y=0,x=0), as shown in the accompanying figure.
In the y = a + bx equation, a is called the y-intercept and b is called the slope. A perfect relationship between y and x will have an intercept of zero and a slope of one. The graph of this relationship is very familiar and shows a straight line making a 45-degree angle with the base of the graph and passing through the zero point (y=0,x=0), as shown in the accompanying figure.
This kind of "comparison graph" is commonly used to present data from a comparison of methods experiment, where a group of specimens (usually 40 or more) are measured by a new or test method and an established method or comparitive method. Ideally, the data should demonstrate a straight line relationship with a 45 degree angle and a zero intercept. Such a one-to-one linear relationship would have a slope of one. As A increases one unit, B should increase one unit. Statistical computer program are available to perform these calculations, present the slope and intercept values, and provide a plot of the data. [For example, see the paired-data calculator that is part of the internet tools available on this website.]
Correlation vs regression
Both correlation and regression statistics are commonly calculated for sets of data that expected to show a linear relationship, e.g., method comparison studies where it is of interest to know how the values obtained from a new method or instrument relate to those from the old method or instrument. A correlation coefficient close to +1.00 shows that y increases whenever x increases. However, the exact amount of the increase isn't clear, e.g., a change of 5 units in x may correspond to a change of 10 units in y. To describe exactly how much y will change as x changes, we need to know the regression statistics - the slope and y-intercept. Then, using the equation for a straight line (y = a + bx), we can calculated the expected y-value for any chosen x-value. Regression, therefore, is a much more useful statistical tool than correlation because it allows you to predict the exact y-value that corresponds to a chosen x-value.
Summary
The Lessons 2 and 3 and the "organizer" figure are be used as a guide or a map. It should be helpful to refer back to these materials, particularly the organizer figure, as you move through the ongoing lessons. The organizer tells you not only about the organization of the course, but also about the relationship between different statistics. It will help you monitor your progress through the course and your understanding along the way. It shows you how to organize the statistics and gain power over the concepts. Those are the capabilities that will help you apply statistics to real data and real problems in the future.
About the author: Madelon F. Zady
Madelon F. Zady is an Assistant Professor at the University of Louisville, School of Allied Health Sciences Clinical Laboratory Science program and has over 30 years experience in teaching. She holds BS, MAT and EdD degrees from the University of Louisville, has taken other advanced course work from the School of Medicine and School of Education, and also advanced courses in statistics. She is a registered MT(ASCP) and a credentialed CLS(NCA) and has worked part-time as a bench technologist for 14 years. She is a member of the: American Society for Clinical Laboratory Science, Kentucky State Society for Clinical Laboratory Science, American Educational Research Association, and the National Science Teachers Association. Her teaching areas are clinical chemistry and statistics. Her research areas are metacognition and learning theory.
