QC Design
Leukocyte Count
A simple example planning QC for hemoglobin using OPSpecs charts.
- Example data
- 1. Define the Quality Requirement
- 2. Evaluate the precision and accuracy of the method
- 3. Look Up OPSpecs Charts
- 4. Plot Operating Point
- 5. Assess probabilities of rejection
- 6. Select the control rules and numbers of control measurements
- 7. Adopt a Total QC Strategy
- 8. Reassess for changes in performance
- Using QC Validator to choose a rule
- For further reading
This month, we're using a leukocyte or white count example to illustrate the application of the QC planning process to select appropriate QC procedures for your laboratory tests. We recommend the 8-step planning process shown below. This process allows you to select control rules and numbers of control measurements (N) to monitor individual tests on the basis of the quality required by the test, the observed accuracy and precision of a method in your laboratory, and the expected error detection and false rejection characteristics of the QC procedure itself.
Example data for this application:
- Test: Leukocyte Count
- Decision level/Target Value: 8 K/uL (i.e. this is where we are running one of the controls because this is an important level for test interpretation)
- Imprecision SD: 0.312 K/uL
- Inaccuracy (bias): 0 K/uL
- Number of control materials: 3 (that is, we intend to analyze three different concentrations or levels of control materials)
1. Define the quality requirement.
Each individual test has its own quality requirements in clinical or analytical terms. For practical purposes, the CLIA proficiency testing criteria for acceptability provide the minimum total error requirements for all regulated tests. For example, the total error that is allowable for a leukocyte count method at a decision level or target value of 8 K/uL is 15%. This means a test result should be correct within 1.2 K/uL.
2. Evaluate the precision and accuracy of the method.
Method performance can be assessed from initial method evaluation studies, on-going validation studies, and current performance on internal and external control materials. It is best that these performance characteristics reflect how the method works in your laboratory, however, estimates can also be obtained from evaluation studies in the literature and from manufacturer’s claims in product labeling. In this example, our leukocyte count method has a 0.312 K/uL SD and no bias.
The method imprecision and bias should be expressed in percentages to use OPSpecs charts. Use the decision level (the level at which you run controls, a target value where a small change becomes important, etc.) as a basis for calculation. For leukocyte count, this level is 8 K/uL. Now if your SD is 0.312 K/uL, then the %CV is 0.312/8 = 3.9%. The calculation for bias is easy - if there is no bias, then the % bias is 0.
3. Look up OPSpecs charts.
For a lesson on OPSpecs charts, click here.
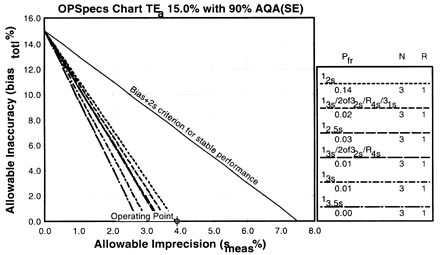
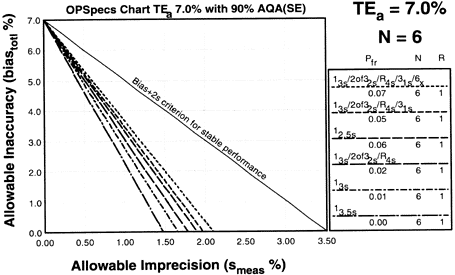
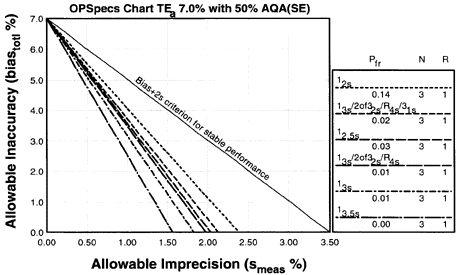
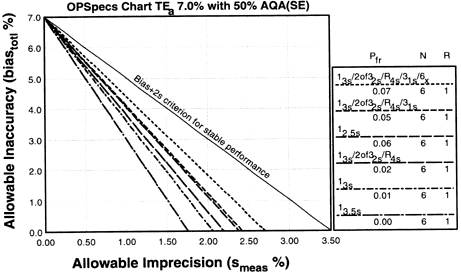
Since the analytical quality requirement is 15%, we should look at OPSpecs charts for a 15% allowable total error, or TEa. Furthermore, if the instrument for our method runs three control materials, then we want to look at control rules with numbers of measurement (N's) of 3 and 6. Thus, we want to look at OPSpecs charts for a 15% analytical quality requirement and N's of 3 and 6. There are several ways to obtain these OPSpecs charts. For those with a computer, the QC Validator program will produce OPSpecs charts for any quality requirement and three different levels of error detection (90% AQA, 50% AQA, and 25% AQA). For this example, however, we are going consult an OPSpecs Manual, which is a library of OPSpecs charts for common control rules and quality requirements. An index of charts tells us that we can find the relevant OPSpecs charts on pages 3-74 and 3-75 of the OPSpecs Manual, Expanded Edition. A two page layout displays 4 OPSpecs charts in the following order:
 |
 |
 |
 |
The objective is to achieve 90% error detection with the lowest N possible. Thus, you start by looking at OPSpecs chart with the highest error detection and lowest N.
| Again we plot the operating point at (x=3.9, y=0). Notice any difference this time? There are three lines above the operating point. |
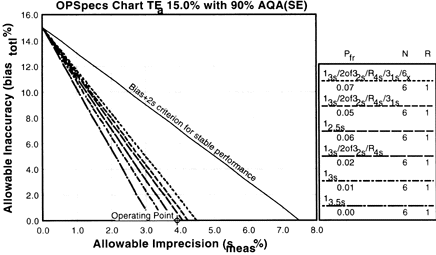
|
5. Assess the probabilities for rejection.Check the key at the right of the graph to match up the lines that passed above your operating point with the control rules and N's they represent. Note the column labelled Pfr lists the false rejection of each control rule. Ideally, you want to aim for a Pfr of 5% or less. |
|
6. Select the control rules and number of control measurements.
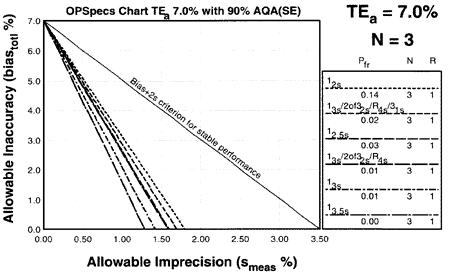
In our example, we have three choices:
- The multirule 13s/2of32s/R4s/31s/6x multirule with 7% false rejection,,
- The multirule 13s/2of32s/R4s/31s multirule with 5% false rejection, or
- The single rule 12.5s with 6% false rejection.
The first multirule is a 13s/2of32s/R4s/31s/6x with N=6 and has a 7% false rejection rate. The rule is probably too complicated for most laboratories, but more importantly, it has a high false rejection rate. The second multirule is a 13s/2of32s/R4s/31s with N=6 and has a 5% false rejection rate. This is not bad, but it is still complicated. The third QC procedure, 12.5s has a 6% false rejection rate -- which is a little high but it has the advantage of being simple to implement.
Conclusion: The 12.5s single rule with N=6 is the best choice for this method. It provides more than 90% error detection with 6% false rejection. This is the control rule we choose for the method.
Note:In situations where 90% error detection cannot be achieved by increasing N and/or using multirule criteria, then you may consider optimizing performance for the observed or expected stability of the process (frequency of errors). Consider 50% error detection for moderately stable processes. Consider 25% error detection for highly stable processes that seldom have problems.
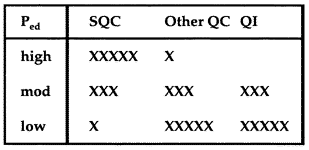
7. Adopt a total QC strategyThe Total QC strategy includes statistical QC, as well as other QC components such as preventive maintenance, system function checks, measurement validation tests, patient data QC, and finally quality improvement. The appropriate balance of these TQC components can be decided based on the error detection that is available from your statistical QC procedure. |
|
If Ped is high, 0.90 or greater, you can depend on statistical QC to detect problems, therefore perform the minimum other QC that is required by government regulations, accreditation standards, manufacturer's instructions, and good laboratory practice. If Ped is moderate, 0.50 or greater, balance your efforts between statistical QC and other QC; also attempt to improve the performance of the method (QI) by reducing any bias and minimizing the standard deviation of the method. If Ped is low, less than 0.50, you will need to depend primarily on other QC and should make a serious effort to improve method performance, possibly even replacing your method with a new and better method.
Conclusion: In our example, we achieved high error detection (greater than 90%) and acceptable false rejection (6%), with an N of 6. Therefore, we can rely on statistical QC, so we choose a High Ped TQC strategy. Even though the method can be well controlled, it would be desirable to improve method performance in order to reduce the number of control measurements that are needed and therefore reduce the cost of this testing process.
For more information about TQC strategies, click here.
8. Reassess for changes in performance.
This QC planning process should be repeated whenever there are changes in the performance of the method. If performance improves, it may be possible to widen the control limits or lower the N. If performance deteriorates, it may be necessary to increase the amount of QC, increasing N and changing the control rules to narrow our limits, or increasing the rules to form multirule procedures.
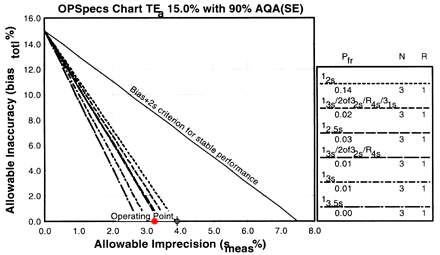 Changes in imprecision and inaccuracy can be examined using the same OPSpecs charts. For instance, if the CV could be reduced to around 3.2%, we can assess its QC effects by plotting a new operating point of (3.2, 0.0; red dot) on the first OPSpecs chart we tried. With this new imprecision, it would be possible to control the test with a 13s/2of32s/R4s/31s multirule, a 13s/2of32s/R4s multirule, or a 12.5s. All of these rules have much lower false rejection and have N of 3 instead of 6. So by reducing the CV by less than a percent, you can half the number of control measurements you would need to make. What would happen if the CV could be reduced to 2.5%?
Changes in imprecision and inaccuracy can be examined using the same OPSpecs charts. For instance, if the CV could be reduced to around 3.2%, we can assess its QC effects by plotting a new operating point of (3.2, 0.0; red dot) on the first OPSpecs chart we tried. With this new imprecision, it would be possible to control the test with a 13s/2of32s/R4s/31s multirule, a 13s/2of32s/R4s multirule, or a 12.5s. All of these rules have much lower false rejection and have N of 3 instead of 6. So by reducing the CV by less than a percent, you can half the number of control measurements you would need to make. What would happen if the CV could be reduced to 2.5%?
Using QC Validator (and automatic QC selection):If we had used QC Validator for the original example, we would have entered all the example data into the parameters screen. |
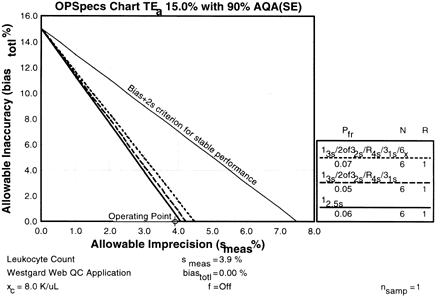 After entering the data, you click the 3 Materials button. (Why the 3 Materials button? Because you are running three levels of control.) Through automatic QC selection, Validator also chooses the 12.5s control rule with N of 6 (indicated by the solid black line in the graph and the key; the other rules have dotted or dashed lines). It's the same rule you selected using manual inspection of OPSpecs charts, but Validator has done the work for you (and in one step instead of two). Validator also displays the other two control rules that are possible choices if you decide not to use the 12.5s control rule.
After entering the data, you click the 3 Materials button. (Why the 3 Materials button? Because you are running three levels of control.) Through automatic QC selection, Validator also chooses the 12.5s control rule with N of 6 (indicated by the solid black line in the graph and the key; the other rules have dotted or dashed lines). It's the same rule you selected using manual inspection of OPSpecs charts, but Validator has done the work for you (and in one step instead of two). Validator also displays the other two control rules that are possible choices if you decide not to use the 12.5s control rule.
For Further Reading
- Westgard JO. "Assuring analytical quality through process planning and quality control." Arch Pathol Lab Med 1992;116:765-769.
- Westgard JO. "Charts of operational process specifications (‘OPSpecs charts’) for assessing the precision, accuracy, and quality control needed to satisfy proficiency testing performance criteria." Clin Chem 1992;38:1226-1233.