Basic Method Validation
Basic validation of qualitative tests
In this first lesson, Dr. Paulo Pereira introduces some of the basic concepts of method validation that apply when a qualitative method is being evaluated.
Basic Validation of Qualitative Tests
Paulo Pereira, PhD
November 2016
Introduction
The validation of qualitative tests differs from the quantitative tests principally since there are no numerical results but binary results, e.g., positive/negative result. Immediately these tests are recognized in medical laboratories according to this designation. However, they could be related to nominal quantities or ordinal quantities [1]. Ordinal quantities are linked to the “pure” qualitative test result, where only a binary condition is known. Nominal quantities are related to binary results arising from the comparison of a numerical quantity results on an ordinal scale considering a certain decision point or “cutoff.” Sometimes in medical laboratories terminology, nominal tests are referred as qualitative - e.g., agglutination/positive/no-agglutination/negative in a slide, number of crosses of an observed certain reagent - and ordinal tests as semi-quantitative - e.g., positive result given that 4.12 is equal or higher than the “cutoff”=1.00. The validation concepts in this essay only deal with the final binary result that can be applied to any qualitative test. The cases in this lesson use virology results. However, the concepts can be applied to any other qualitative test.
Purpose
Verification and validation definitions are sometimes confusing in practice. ISO defines verification as the “confirmation, through the provision of objective evidence, which specified requirements had been fulfilled” (3.8.12 of [2]). Validation is defined as the “confirmation, through the provision of objective evidence, that the requirements for a specific intended use or application have been fulfilled” (3.8.13 of [2]). In contrast to the verification explanation, validation is directly related to the interested parties requirements, such as the accuracy of clinical decision required by the patients. Erroneous binary results, i.e., false results, affect the clinical decision directly. Therefore, the qualitative test validation goal is to confirm, based on data, that the requirements for its use have been fulfilled. These specifications should be intended to assure a nonsignificant risk of false results.
The approach
Rev. Reverend Thomas Bayes (1702-1761) developed a probabilistic model for defining the likelihood that an element would be a member of a specific class. On a qualitative test view, the element is the binary result, and the class is the disease or nondisease group of subjects. So, the model determines the probability of a patient or a healthy individual to be truly classified as infected or noninfected. This classification is referred as diagnostic sensitivity Se[%] when “the percentage (number fraction multiplied by 100) of subjects with the target condition (as determined by the diagnostic accuracy criteria) whose test values are positive”, and diagnostic specificity Sp[%] when “the percentage (number fraction multiplied by 100) of subjects without the target condition (as determined by the diagnostic accuracy criteria) whose test values are negative” (5.3 of [3]).
The comparison of methods can be determined primarily when the comparator is the diagnostic accuracy criteria, or it can be determined secondarily when the comparator is other than the diagnostic accuracy criteria. The primary design is a diagnostic accuracy model intended to measure “the extent of agreement between the information from the test under evaluation and the diagnostic accuracy criteria” (5.3 of [3]). The area under the receiver operating characteristic (ROC) curve is another diagnostic accuracy measurement, complementary to the sensitivity and specificity [4].
Sampling
The patient samples for this validation should be taken from the target population. A representative sampling of infected individuals can be difficult to obtain for a virology qualitative test. The sources of uncertainty in chemistry tests are related principally to the pre [5] and the analytical phase, to the intra- and inter-individual variation, and to the effects of diseases [6], drugs [7] and herbs and natural products [8]. In a virology tests, however, several additional sources variation can affect the accuracy of the results, such as the types and sub-types of the agent, mutations [9], and the seronegative window period [10]. Sometimes to obtain a “complete” sampling requires the use of commercial panels. Note that the infected individual sampling must only have samples from diagnosed individuals. If the only available samples are from patient samples with a known result from another screening test, this uses the secondary model.
Samples from noninfected individuals are much easier to obtain. However, there should be evidence that the individuals are healthy/noninfected. Regular blood donors are an example of a suggested population. In this sampling, the target population is the set of generic healthy individuals.
The number of samples is a limitation to the statistical power of the study. As many samples should be used as is practical. If the number of samples does not affect the fixed percentage directly, its influence is critical to the 95% confidence interval (95% CI). The laboratorian should understand this limitation when defining the specifications. For instance, the sensitivity confidence interval to n = 5, could not be smaller than 56.6 to 100%. This example also shows the limit of this sampling’s n to the confidence interval - the statistical power of the estimate is poor.
Duration
CLSI EP12-A2 suggests the study be performed over the course of 10 to 20 days [3]. The laboratorian can choose a shorter period. However, the reproducibility conditions of the study should be assured to reliable estimates.
The methods
1. When the comparator is the diagnostic accuracy criteria.
There is commercial statistical software available to support this study. Nevertheless, the determination can easily be performed in a spreadsheet. The worktable in this method is a 2x2 contingency table where positive and negative results from candidate test are measured “against” diagnostic accuracy criteria. Table 1 shows a 2x2 contingency table and the equations to determine the diagnostic sensitivity and specificity. Complementary measurements can be performed, but their importance to the validation is minor. For instance, the efficiency of the test’s results E[%] (4 of [11]) which shows the percentage of true results, and the prevalence of positive and negative results (5.3 of [3]). From the laboratorian's viewpoint, the sensitivity and specificity are the critical determinations. From the physician's perspective, the core measurements are the prediction values since they describe the probability of a result to accurately diagnose a subject. It could be determined the positive predictive value (percentage) PPV[%] and the negative predictive value (percentage) NPV[%] (5.3 of [3]) (see Table 1).
The inference of the results for the 95% confidence interval can easily be calculated in a spreadsheet. See Table 1 for equations to the sensitivity and specificity low limit (LL) and high limit (HL). The laboratorian should understand that this inference is limited by the characteristics of the samples. Consequently, if the sampling diagnostic accuracy is biased, the confidence interval is also.
Case study 1:
Let assume that the number of infected individuals is 24 and the number of healthy subjects is 96. The number of true positive results is 24, and the number of true negative results is 94. Accordingly:
Se[%]=24/(24+0)x100=100%; 95% CI:
A1=2x24+1.962=51.8;
A2=1.96(1.962+4 x24x0/(24+0))1/2=3.8, and;
A3=2(24+0+1.962)=55.7;
SeLL[%]=(51.8-3.8)/55.7x100=86%;
SeHL[%]=(51.8+3.8)/55.7x100=100%.
Consequently, True Positive lies within the interval [86%, 100%]
Sp[%]=94/(94+2)x100=98.1%; 95% CI:
B1=2x94+1.962=191.8;
B2=1.96(1.962+4 x94x2/(94+2))1/2=6.7, and;
B3=2(94+2+1.962)=199.7;
SpLL[%]=(191.8-6.7)/199.7x100=93%;
SpHL[%]=(191.8+6.7)/199.7x100=99%.
Therefore, True Negative lies within the interval[93%, 99%]
The goals: Se[%]=100%, True Positive should be within [75%, 100%], and ; Sp[%]=95%, True Negative should be within [75%, 90%]
In this example, the candidate test can be accepted since all specifications are met. Note that the specified goals should consider the intnded use of the results. For instance, in a blood bank, the sensitivity is the critical measurement since it affects directly the chance of a blood receptor to receive a false negative blood component. In the medical laboratory, this specification is not so critical since there is not a secondary our secondaries subject(s) involved.
Pros of this approach:
- Easier to implement in the medical laboratory since the diagnosis is known
- Diagnostic accuracy estimate: diagnostic sensitivity and specificity
- 95% CI measurement
Cons of this approach:
- A large number of samples is required for robust statistical power
- The seronegative window period is a component of the residual risk
- Most of the time commercial panels are needed
- It could be expensive compared to the concordance of the results model
- No traceable materials

TP: true positive results; TN: true negative results; FP: false positive results; FN: false negative results; n: total number of samples
Se[%]=TP/(TP+FN)x100;
SeLL[%]=(A1-A2)/A3x100; SeHL[%]=(A1+A2)/A3x100; A1=2xTP+1.962; A2=1.96(1.962+4 xTPxFN/(TP+FN))1/2; A3=2(TP+FN+1.962)
Sp[%]=TN/(TN+FP)x100;
SpLL[%]=(B1-B2)/B3x100; SpHL[%]=(B1+B2)/B3x100; A1=2xTN+1.962; A2=1.96(1.962+4 xTNxFP/(TN+FP))1/2; A3=2(TN+FP+1.962)
E[%] = TP+TN/n x100; PPV[%]=TP/(TP+FP) x100; NPV[%]=TN/(TN+FN)x100
2. When the comparator is other than the diagnostic accuracy criteria
This alternative approach should be used only when samples from diagnosed or healthy subjects are unavailable. The comparator test results should have a diagnostic accuracy meeting the medical laboratory specifications. The measurement directly depends on these results. For instance, if the comparator has a worse performance than the new test, the validation could be misinterpreted. All discrepant results should be evaluated using a confirmatory scheme.
Concordance and disagreement are substituted for the terms true and false positive and negative, respectively. Consequently, diagnostic sensitivity and specificity are replaced by positive concordance PC[%] and negative concordance NC[%], respectively. The PC[%] is the percentage (number fraction multiplied by 100) of positive results whose comparator test values are positive. The NC[%] is the percentage (number fraction multiplied by 100) of negative results whose comparator test values are negative. The overall concordance OC[%] is complementary to these measurements and related the concordance of results with the total number of results. See Table 2 for mathematical equations. To compute the 95% CI the equations are analogous to the Table 1 calculations.
Case study 2:
Let assume that the number of positve results in a comparative test is 32 and the number of healthy subjects is 94. All the results are concordant. Accordingly:
PC[%]=32/(30+2)x100=100%; 95% CI:
C1=2x32+1.962=67.8;
C2=1.96(1.962+4 x32x0/(32+0))1/2=3.8, and;
C3=2(32+0+1.962)=71.7;
SeLL[%]=(67.8-3.8)/71.7x100=89%;
SeHL[%]=(67.8-3.8)/71.7x100=100%.
Consequently, a is within the interval [80%, 98%]
NC[%]=94/(94+0)x100=100%; 95% CI:
D1=2x94+1.962=191.8;
D2=1.96(1.962+4 x94x0/(94+0))1/2=3.8, and;
D3=2(94+0+1.962)=195.7;
SpLL[%]=(191.8-3.8)/195.7x100=96%;
SpHL[%]=(191.8+3.8)/195.7x100=100%.
Therefore, d is within the interval [96%, 100%]
The goals: PC[%]=100%, a should fall within [75%, 100%]; NC[%]=95%, d should fall within [75%, 90%]
For this example, the candidate test is acceptable since specifications for the positive and negative concordance are being met. Note that in this case only samples with confirmed results should be used. Otherwise, the concordance could be significantly biased.
Pros of this approach:
- Use of an old assay as comparative assay
- The seronegative window period is a component of the residual risk
- No need for commercial panels
- It could be inexpensive compared to the diagnostic accuracy model
- 95% CI measurement
Cons of this approach:
- Harder to implement in the medical laboratory since the diagnosis is unknown
- No diagnostic accuracy criteria: diagnostic sensitivity and specificity cannot be estimated
- A large number of samples is required for significant statistical power
- No traceable materials
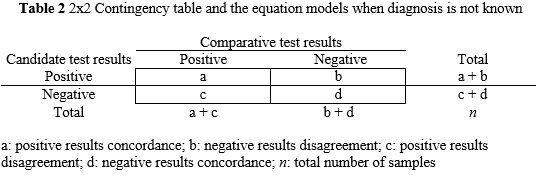
a: positive results concordance; b: negative results disagreement; c: positive results disagreement; d: negative results concordance; n: total number of samples
PC[%]=a/(a+c)x100; NC[%]=d/(d+b)x100;OC[%]=(a+d)/nx100
Conclusion
The validation of quantitative tests should be clearly understood by the laboratorian to identify what is measured and what is not. Some sources of error cannot be combined on the final estimate due to the limitations of the study - e.g., lack of a commercial panel with rare subtypes, sampling not representative of the population. However, the seronegative window period is a systematic weakness in this validation. The determination of the window period should be complementary to this study, and it is the principal source of the residual risk of false negatives. Note that the window period is the seronegative period for a certain individual, and not the window period of a population. For an application of this essay’s principles to screening POCT see [12].
References
- Bureau International des Poids et Mesures (2012). JCGM 200:2012 International Vocabulary of Metrology-Basic and General Concepts and Associated Terms, 2008 version with minor corrections. 3rd ed. Sèvres: BIPM. Retrieved from: http://www.BIPM.org/utils/common/documents/jcgm/JCGM_200_2012.pdf. Accessed: November 11, 2016.
- International Organization for Standardization (2015). ISO 9000 Quality management systems - Fundamentals and vocabulary. 3rd ed. Geneva: ISO.
- Clinical and Laboratory Standards Institute (2008). EP12-A2 User Protocol for Evaluation of Qualitative Test Performance. 2nd ed. Wayne (PA): CLSI.
- Pereira P, Westgard JO, Encarnação P, Seghatchian G (2015). Evaluation of the measurement uncertainty in screening immunoassays in blood establishments: Computation of diagnostic accuracy models. Transfus Apher Sci 52(1):35-41.
- Young D (2007). Effects of Preanalytical Variables on Clinical Laboratory Tests. 3rd ed. Washington (DC): AACC Press.
- Young D (2001). Effects of Disease on Clinical Laboratory Tests. Volumes 1 & 2. 4th ed. Washington (DC): AACC Press.
- Young D (2000). Effects of Drugs on Clinical Laboratory Tests. Volumes 1 & 2. 5th ed. Washington (DC): AACC Press.
- Narayanan S, Young D (2007). Effects of Herbs and Natural Products on Clinical Laboratory Tests. Washington (DC): AACC Press.
- Müller B, Nübling C, Kress J, Roth W, De Zolt S, PichlL (2013). How safe is safe: new human immunodeficiency virus type 1 variants missed by nucleic acid testing. Transfusion 53(10): 2422-2430.
- Pereira P, Westgard JO, Encarnação P, Seghatchian G (2014). Analytical model for calculating indeterminate results interval of screening tests, the effect on seroconversion window period: A brief evaluation of the impact of uncertain results on the blood establishment budget. Transfus Apher Sci 51(2):126-131.
- Clinical and Laboratory Standards Institute (2002). EP12-A User Protocol for Evaluation of Qualitative Test Performance. Wayne (PA): CLSI.
- Pereira P. Evaluation of rapid diagnostic test performance. In book: Saxena SK (editor). Proof and concepts in rapid diagnostic tests and technologies. Rijeka: InTech.
