QC Design
The Meaning and Application of Total Error
While the scientific community has grown comfortable with the once-revolutionary concept of "total error", novices and newcomers are often puzzled by the term. Dr. Westgard answers a few "back to basics" questions about total error and its role in laboratory testing.
April 2007I was recently asked about the meaning of total error and how it fit together with precision and bias, which are the classical performance characteristics of a measurement procedure. Specifically, the questions asked the following:
- What is the definition of total error?
- How should the bias (inaccuracy) and the standard deviation (imprecision) be determined?
- What confidence level or z-value should be used as the multiplier of the SD in the calculation of TE?
- What is the practical application of total error?
The Short Answer
Total error, TE, represents the overall or total error that may occur in a test result due to both the imprecision (random error) and inaccuracy (systematic error) of the measurement procedure. It is commonly defined as TE = Bias + Z*SD, where bias is the estimate of systematic error, SD is the estimate of random error, and Z is the multiplier that represents the desired confidence level.
The bias and SD may initially be estimated from method evaluation studies – bias from the comparison of methods experiment and SD from a replication experiment. Later on, after implementation a new measurement procedure, the SD may be estimated from the monthly QC data and bias from peer comparison programs, External Quality Assessment (EQA) surveys, or Proficiency Testing (PT) results. The analyst needs to exercise scientific judgment on the best sources of data that are available at the time.
Different recommendations have been made for the Z-value, ranging from 2 to 6. Most commonly, a Z-value of 2 is used in the reports from peer comparison programs, whereas in method validation studies, multiple values can be considered when using a “Method Decision Chart.”
The intended use of total error is to describe the maximum error that might occur in a test result obtained from a measurement procedure. In method validation studies, it provides a measure of quality that can be compared to the intended analytical quality of a test, which can be described in terms of an allowable total error (TEa). TEa is an analytical quality requirement that sets a limit for both the imprecision (random error) and bias (systematic error) that are tolerable in a single measurement or single test result.
A second use has developed over time. Peer-comparison programs often calculate the total error on the basis of the SD observed on internal QC materials and the bias on the basis of the lab’s mean versus some overall mean for a method subgroup or the mean from the total peer group. This estimate of total error is intended to be predictive of the variation expected in the test results delivered to the physician users and patient consumers. In this context, total error might be thought of as a precursor of today’s measurement uncertainty, but estimated by a top-down approach rather than the bottom-up estimate recommended by ISO/GUM.
Some additional perspective
These questions take me back to the early years of my career in clinical chemistry when I was very concerned with developing a reliable protocol for evaluating the performance of new measurement procedures.
From my training in analytical chemistry, I understood the evaluation experiments and their use for estimating different types of analytical errors, e.g., use of the replication experiment for estimating random error or imprecision, the interference experiment for estimating specific causes of constant systematic errors the recovery experiment for estimating proportional interference, and comparison to a reference method for estimating the systematic errors or inaccuracy in the typical population of specimens.
One of the most difficult issues was how to make a judgment about the acceptability of a new measurement procedure. At that time, people often made use of the correlation coefficient and statistical tests of significance, such as t and F. That just didn’t make any sense to me, so I adopted a different approach which was to use the statistical calculations to estimate the size of the errors that were being uncovered by the different validation experiments [1]. The decision on the acceptability then became one of judging the importance of those observed errors relative to the amount of error allowable in the intended clinical application of the diagnostic test [2]. This provided a rational and objective framework for making judgments about the acceptability of new measurement procedures. Most important, it made sense to the clinical laboratory scientists who were responsible for performing these studies in the laboratory.
An important consideration was whether to judge acceptability on the basis of separate components of error, such as the observed SD or the observed bias, or whether to consider the combined or total effect of both the SD and the bias. In effect, we were faced with applying a new and different concept of accuracy – the overall error concept of accuracy or total error of a test, rather than the systematic error concept of accuracy which prevailed at that time. This overall concept of accuracy is illustrated in the accompanying figure.
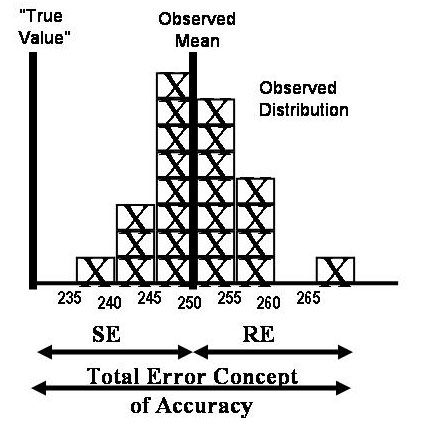
At the time of the introduction of the total error concept in 1974, we recommended a Z-value or multiplier of 2, i.e., TE = bias +2SD. In 1990, Ehrmeyer and Laessig [3] recommended a multiplier of 3 based on the performance required to pass proficiency testing when a laboratory is subject to PT for 20 different tests. That same year, working with Bob Burnett at Hartford Hospital, we recommended the multiplier be 4 or higher in order for the laboratory to be able to properly control their measurement procedures [4]. Finally, as Six Sigma Quality Management emerged in the late 90s, it became apparent that the 6-sigma goal for World Class Quality meant that the multiplier could be as high as 6 [5].
Keep in mind that the primary purpose was to judge the acceptability of a measurement procedure for application in a routine service laboratory (the method evaluation application), not to express the possible range of values that might be associated with a given test result (the uncertainty application). To judge acceptability, we recommend use of a graphical tool called the Method Decision Chart which incorporates TE criteria for 3s, 4s, 5s, and 6s [6], as shown in the accompanying figure.
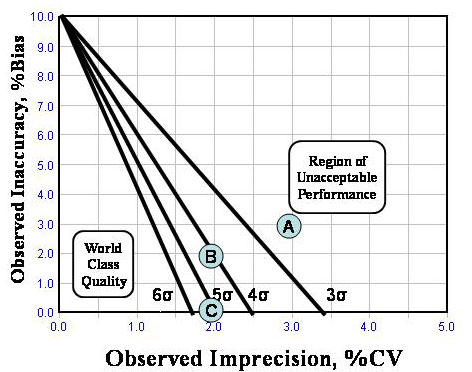
To prepare this chart, the analyst first defines TEa, then scales the y-axis from 0 to TEa and the x-axis from 0 to 0.5TEa, e.g., in this example, TEa is 10%, which happens to be the CLIA criterion for acceptable performance for a cholesterol method. To apply this chart, the analyst then plots an operating point whose y-coordinate represents bias (expressed as a percentage) and the x-axis represents the CV of the measurement procedure. Point A represents a method having a 3.0% bias and 3.0% CV, which actually are the maximum allowable performance specifications set by NCEP for cholesterol. Such a method provides less than 3-sigma quality, which would not generally be acceptable for an industrial production process. Point B represents 2.0% bias and 2.0% CV, or 4-sigma quality, which is acceptable and manageable in a clinical laboratory. Point C represents 0% bias and 2.0% CV, which is a 5-sigma process and could be more easily managed (less QC needed) in a clinical laboratory.
What’s the point?
Precision and accuracy (or imprecision and inaccuracy, or random and systematic errors) are performance characteristics of the measurement procedure for which manufacturers generally make claims and governments often require verification by the laboratory. Total error describes the quality of a test result, providing a worst case estimate of how large the errors might be in a single measurement. Manufacturers generally do not make any claim for quality, thus total error is mainly used in the laboratory to judge the acceptability of a measurement procedure for its intended use.
In short, total error is a quality characteristic whereas precision and accuracy are performance characteristics that contribute to the quality of a test result. Different combinations of precision and accuracy can produce the same quality for a test result, thus it is better to set goals for the allowable total error, rather than set individual goals for the allowable SD and the allowable bias.
References
- Westgard JO, Hunt MR. Use and interpretation of common statistical tests in method-comparison studies. Clin Chem 1973;19:49-57.
- Westgard JO, Carey RN, Wold, S. Criteria for judging precision and accuracy in method development and evaluation. Clin Chem 1974;20:825-833.
- Ehrmeyer SS, Laessig RL, Leinweber JE, Oryall JJ. 1990 Medicare/CLIA final rules for proficiency testing: Minimum interlaboratory performance characteristics (CV and bias) needed to pass. Clin Chem 1990;36:1736-1740.
- Westgard JO, Burnett RW. Precision requirements for cost-effective operation of analytical processes. Clin Chem 1990;36:1629-1632.
- Westgard JO. Six Sigma Quality Design and Control, 2nd ed. Madison WI:Westgard QC, Inc., 2006.
- Westgard JO. Basic Method Validation, 2nd ed. Madison WI:Westgard QC, Inc. 2003, Chapter 16, pp 173-182.
James O. Westgard, PhD, is a professor emritus of pathology and laboratory medicine at the University of Wisconsin Medical School, Madison. He also is president of Westgard QC, Inc., (Madison, Wis.) which provides tools, technology, and training for laboratory quality management.
