QC Design
Is this the End of QC as we know it? And end of EQA and PT, too?
It's 2021, the new year, so of course it's time for someone to suggest a new way to do QC. This time it's the metrologists, and their proposal has a few merits and many more downsides.
Metrologists are Rethinking IQC - Wrongly
January 2021
James O. Westgard, Sten A. Westgard
Recommendations for changing the structure of Internal Quality Control have recently been published as a summary from a 2019 conference that focused on metrological traceability and IQC [1]. In the new formulation, IQC is divided into two parts which require different control materials. IQC Component I applies to traditional non-traceable control materials that are used to monitor analytic performance and make decisions to accept or reject analytical runs. IQC Component II requires a new traceable and commutable control that is analyzed once per day over a period of 6 months for the purpose of estimating measurement uncertainty (MU). There is also new guidance for interpreting IQC component I, establishing validation limits, emphasizing longitudinal QC evaluation, and recommending the use of an “acceptability range” as derived from the Milan models for establishing Analytical Performance Specifications (APS).
We call your attention to these recommendations because we expect they will, at some time in the future, be adopted as official dogma by the European Federation for Laboratory Medicine (EFLM), which has been heavily promoting metrological concepts such as measurement uncertainty (MU). This SQC development relates to the recommendations from the 2014 Milan Conference [2] on Analytical Performance Specifications, which revised the approaches the 1999 Stockholm Conference.
We have discussed some of the issues earlier on this website, particularly the EFLM recommendations to replace Total Error goals that apply to both imprecision and bias with separate goals for precision (in the form of allowable MU) and bias. We also have concerns about the correction of bias which is implicit in the adoption and application of the metrology theory. See reference 3 for more discussion of errors methods vs uncertainty methods.
A side note: Is the Future of QC Traceable? Does it mean the end of PT/EQA?
By proposing a new kind of control material, we have to wonder where the funds to purchase two sets of control materials are going to come from. Are labs really going to run regular controls and traceable controls? How will labs afford this? Why not just use the traceable control to determine both imprecision and bias. For all the desire of the metrologists to separate bias and imprecision into two components, two controls, it's probably a bit more cost-effective to allow one control to do both.
Another question that follows naturally – if these future traceable controls can help us determine both the bias and imprecision of methods, why do we have to bother with external quality assessment through another program?
Why perform proficiency testing two to three times a year, if traceable controls can provide the necessary service on a daily basis. If control vendors are looking to expand their utility, service, (and support their continuing price increases), then this is a useful path for them to take. If we are contemplating a future where there are fewer expenses for the laboratory, which service – EQA or QC – is going to survive? Can one supplant the other? If daily controls become traceable, there is a good chance those controls can crowd EQA programs out of the market.
But let's step back from the business issues, and return to the scientific ones.
Non-standard SQC terminology
Our primary concern with this paper relates to its lack of understanding of SQC fundamentals. It is not our intent here to provide a thorough review of all the issues with the new formulation of IQC (there are quite a few articles here that provide that), but it is important to challenge the approach before it gains a larger audience. So we will just concern ourselves here with the term “acceptability range”, which is not recognized in the standard terminology for metrology, ISO or SQC. For example, the CLSI C24-Ed4 document [4] whose title includes the words “Principles and Definitions” states “CLSI recognizes its important role… on the harmonization of terms to facilitate the global application of standards and guidelines” and proceeds to provide definitions for some 35 terms that are used in the document, does not include “acceptability range.”
The authors describe “acceptability range” as follows:
“…the acceptability range, which defines the tolerance of value deviation from the target, should permit suitable application of test results in clinical conditions. Information reported on QC data sheets show that the acceptability range provide by manufacturers is usually based on the statistical dispersion of data obtained by n laboratories (e.g., ±2SD or ±20% of the mean value), with no relationship with clinically suitable APS. Sometimes data from interlaboratory programs are used in the determination of validation range, with the risk to include results from laboratories working under biased analytical conditions, and quite often both mean QC values and ranges are provided only “as guide”, with the recommendation that each laboratory should establish its own acceptability limits.”
Actually, the fundamental principle of SQC is that each laboratory should characterize its own imprecision and use that SD in calculation of control limits. Manufacturers may provide controls with assigned values for the Target Value, useful in the initial start up of controls, but the laboratory should use the mean (and SD) of its own performance when preparing a control chart.
Erroneous SQC concept
Instead, the authors recommend applying an acceptability range based on the specification for allowable MU.
“What is lacking is the link with the new scientific background [for metrological traceability]… To obtain this, the acceptability range for QC component I should correspond to APS for MU derived according to the appropriate Milan model and it should be set based on unbiased target value of the material obtained by the manufacturer as the mean of replicate measurement on the same measuring system optimally calibrated to the selected reference.”
The accompanying graphic shows a comparison of two control charts, one that has control limits based on the manufacturer’s defined limits which are wider than the ASP MU limits shown on the other chart. The MU limits are described as “expanded MU for a coverage factor of 2” which implies 2 times MU for “acceptability limits.” These tighter limits are then used to illustrate that the control data would identify a systematic shift that was not identified by the manufacturer’s wider limits.
But that use of acceptability limits is not correct for SQC applications. The limits on control charts should be derived from a quality requirement as described in C24-Ed4, which also references the Milan models for goal setting. Step 1 in the SQC planning process is to define the quality required for intended use, usually in the form of an Allowable Total Error or TEa goal. That goal then becomes the basis for developing an SQC strategy that identifies the statistical control rules, the number of control measurements, and the frequency of SQC events. The CLSI guideline provides a step by step “roadmap” for deriving an SQC strategy from the defined quality requirement. The description of the planning process (section 5) is some 15 pages, which surely suggests it is not so simple as just drawing control limits that represents MU with a 95% coverage factor as an acceptability range.
All control limits are statistical limits
The issue of using an “acceptability range” of ± 2*MU limits is similar to the problems with “clinical limits” and “fixed limits” that have been encountered previously. We discussed this back in 1994, when the CLIA rules were being finalized and there were conflicting recommendations on how to establish control limits [5]. The mechanics are the same, just draw MU limits (that are supposedly clinically requirement performance) directly on the control charts. In this particular case, it corresponds to setting 2 SD limits where the SD is the allowable MU. But keep in mind, those limits are still statistical limits and the actual statistical control rule can be determined by dividing the control limit by the actual method SD determined in the laboratory. Whatever you call the limits, the math is inescapable.
The rejection characteristics of such statistical control rules are then described by power curves, such as shown in the power function graph below. Note that the probability for rejection is plotted on the y-axis vs. the size of the systematic error on the x-axis (bottom scale) or sigma-metric (top scale). The individual curves represent different control rules and/or different numbers of control measurements (N). The probability of false rejection (P:fr) is determined by the y-intercept of each power curve; the probability for error detection (P:ed) is determined for the critical systematic error that is calculated from the quality requirement, the method SD, and the method bias, and can be represented by a vertical line. The available error detection can then be determined from the intersection of that line with the various power curves.
An example for a 4 sigma test
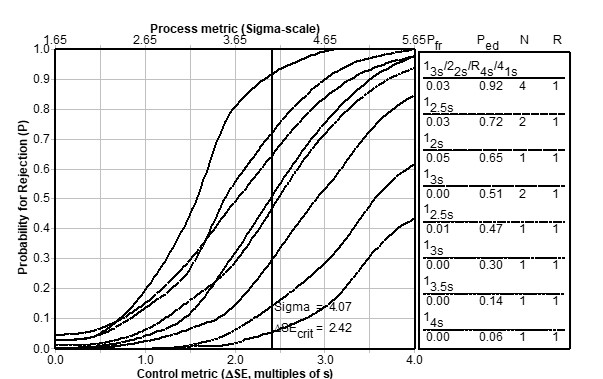
The acceptability range described by the authors likely represents single-rule in the form 1:ns , where an analytical run would be rejected when 1 control observation exceeds the mean ± nSDs. Once we identify the control rule, we can examine its power curve to see the probability of rejection for different size errors.
Let’s consider a specific example, where the acceptance range is described as ±0.4 units for a control with a mean value of 6.5 i.e., the range is from 6.1 to 6.9 units. That acceptance range can be described by a TEa requirement of 6.15% (0.4/6.5). If the actual SD of the method were 0.1 unit, or 1.54% CV, the acceptance range represents a 1:4s control rule (difference of limit from mean divided by SD). If the method has a bias of 0.0 units, the method performs at the 4.07 sigma level [Sigma = (%TEa-|%bias|/%CV) =6.15/1.54), which is represented by the vertical line in the middle of the graph. The SQC performance of a 1:4s rule is described by the bottom line on the graph, which shows the probability of detection of the critical systematic error is only 0.06 or 6%, quite far from the goal of reaching a P:ed of 0.90, a 90% chance of detecting a medically important systematic error. The top curve on the graph shows that the desired error detection can be achieved using a 13s/22s/R4s/41s multirule procedure with 4 control measurements per run.
This illustrates the design of a QC strategy to achieve a defined quality for the intended use of a test. In this case, the numbers in the example correspond closely to a HbA1c test, where performance and SQC are critical for proper patient care.
While a “roadmap” for the SQC planning process can be found in the CLSI C24 guideline [4]. A more detailed step-by-step process using practical graphical tools has been described in the literature [6-8] as well as extensively on the website here.
What’s the point?
A fundamental principle of SQC is that a laboratory should establish the SD that is used for calculating control limits based on data obtained in the laboratory. The idea that a manufacturer sets the acceptability range is itself an erroneous application of SQC. The idea that the laboratory can substitute an APS for an allowable SD that represents the desirable MU is likewise erroneous. In addition, the practice of setting control limits as ±2SD limits is known to provide a high level of false rejections – and we’ve known this for more than 50 years. Thus the recommendation to use a 95% range of the MU goal does not comply with the fundamental principles of SQC practice.
There are many more objections that might raised about the proposed restructuring of SQC practices. The proposed remedy for QC problems is not as simple as suggested, yet there are simple tools available to properly design SQC strategies and practices. Even when applying the rigorous theory of metrology, it is still necessary respect the fundamentals of SQC theory and practice. There may be enormous consequences to restructuring SQC as proposed and the practical benefits of any improved estimates of MU must be weighed against those consequences.
References
- Braga F, Pasqualetti S, Aloisio E, Panteghini M. The internal quality control in the traceability era. Clin Chem Lab Med 2021;59:291-300.
- Special issue: First EFLM strategic conference defining analytical performance goals 15 years after the Stockholm conference. Clin Chem Lab Med 2017;53:829-953.
- Westgard JO. Error methods are more practical, but uncertainty methods may still be preferred. Clin Chem 2018;
4. C24-Ed4. Statistical quality control for quantitative measurement procedures: principles and definitions, 4th ed., Clinical and Laboratory Standards Institute, Wayne, PA, 2016. - Westgard JO, Quam EF, Barry PL. Establishing and evaluating QC acceptability criteria. Med Lab Obs, Feb 1994:3-7.
- Bayat H, Westgard SA, Westgard JO. Planning risk-based SQC strategies: Practical tools to support the new CLSI C24Ed4 guidance. J Appl Lab Med 2017;2:211-221.
- Westgard JO, Bayat H, Westgard SA. Planning risk-based SQC schedules for bracketed operation of continuous production analyzers. Clin Chem 2018;64:289-296.
- Westgard JO, Westgard SA. Establishing evidence-based statistical quality control practices. Am J Clin Pathol 2019;151:364-370.
