Basic Method Validation
Interference and Recovery Experiments
Elsa P. Quam, BS MT(ASCP) joins Dr. Westgard in describing the importance of these two experiments. There are times when comparison methods are not available and experiments for linearity or reportable range and replication are not enough. If your laboratory modifies a manufacturer's method, you need to know how to perform the interference and recovery experiments. Sample data calculations are included.
|
|
| Note: This lesson is drawn from the first edition of the Basic Method Validation book. This reference manual is now in its third edition. The updated version of this material is also available in an online training program accredited by both the AACC and ASCLS. |
Method validation studies for unmodified moderate or high complexity tests tend to focus on the experiments for linearity or reportable range, replication, and comparison of methods, which have been described in previous lessons. However, our experimental plan recommends that interference and recovery experiments also be performed to estimate the effects of specific materials on the accuracy or systematic error of a method. These two experiments are included in the plan because they:
- can be performed quickly to test for specific sources of errors;
- supplement the error estimates from the comparison of methods experiment;
- can be applied when a comparison method is NOT available; and
- are necessary for thorough testing when a manufacturer's method is modified by the laboratory.
Interference and recovery experiments are presented together in this lesson to point out their similarities and their differences.
Interference Experiment
Purpose
The interference experiment is performed to estimate the systematic error caused by other materials that may be present in the specimen being analyzed. We describe these errors as constant systematic errors because a given concentration of interfering material will generally cause a constant amount of error, regardless of the concentration of the sought for analyte in the specimen being tested. As the concentration of interfering material changes, however, the size of the error is expected to change.
Factors to consider
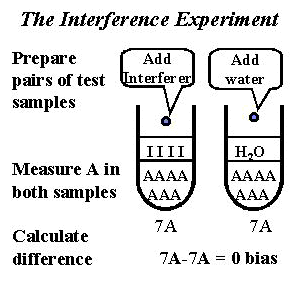 The experimental procedure is illustrated in the accompanying figure. A pair of test samples are prepared for analysis by the method under study. The first test sample is prepared by adding a solution of the suspected interfering material (called "interferer," illustrated by "I" in the figure) to a patient specimen that contains the sought-for analyte (illustrated by "A" in the figure). A second test sample is prepared by diluting another aliquot of the same patient specimen with pure solvent or a diluting solution that doesn't contain the suspected interference. Both test samples are analyzed by the method of interest to see if there is any difference in values due to the addition of the suspected interference.
The experimental procedure is illustrated in the accompanying figure. A pair of test samples are prepared for analysis by the method under study. The first test sample is prepared by adding a solution of the suspected interfering material (called "interferer," illustrated by "I" in the figure) to a patient specimen that contains the sought-for analyte (illustrated by "A" in the figure). A second test sample is prepared by diluting another aliquot of the same patient specimen with pure solvent or a diluting solution that doesn't contain the suspected interference. Both test samples are analyzed by the method of interest to see if there is any difference in values due to the addition of the suspected interference.
Analyte solution. Standard solutions, patient specimens, or patient pools can be used. We recommend a general procedure using patient specimens since they are conveniently available in a healthcare laboratory and contain the many substances found in the real specimen.
Replicates. It is good practice to make duplicate measurements on all samples because the systematic error is revealed by the differences between paired samples. Small differences may be obscured by the random error caused by the imprecision of the method. Making replicate measurements on the pairs of samples, or preparing pairs of samples for several specimens, permits the systematic error to be estimated from the differences in the average values, which will be less affected by the random error of the method.
Interferer solution. For soluble materials, it is convenient to use standard solutions to be able to introduce the interference at a known concentration. For some common interferences, such as lipemia and hemolysis, patient specimens or pools are often used.
Volume of interferer addition. The volume added should be small relative to the original test sample to minimize the dilution of the patient specimen. However, the amount of dilution is not as important as maintaining the exact same dilutions for the pair of test samples.
Pipetting performance. Precision is more important than accuracy because it is essential to maintain the same exact volumes in the pair of test samples.
Concentration of interferer material. The amount of interferer added should achieve a distinctly elevated level, preferably near the maximum concentration expected in the patient population. For example, in testing the ascorbic acid affects on a glucose method, a concentration near 15 mg/dL could be used because this represents the maximum expected concentration [1]. If an effect is observed at the maximum level, then it may also be of interest to test lower concentrations and determine the level at which the interference first invalidates the usefulness of the analytical results.
Interferences to be tested. The substances to be tested are selected from the manufacturer's performance claims, literature reports, summary articles on interfering materials, and data tabulations or databases, such as the extensive tabulation assembled by Young et al [2] which also contains a comprehensive bibliography.
It is also good practice to test common interferences such as bilirubin, hemolysis, lipemia, and the preservatives and anticoagulants used in specimen collection.
- Bilirubin can be tested by addition of a standard bilirubin solution.
- Hemolysis is often tested by removing one aliquot of a sample, then mechanically hemolyzing or freezing and thawing the specimen before removing a second aliquot.
- Lipemia can be tested by addition of a commercial fat emulsion, such as Liposyn (Abbott Laboratories) or Intralipid (Cutter Laboratories), or analyzing lipemia patient specimens before and after ultracentrifugation [3, see procedure recommended by NCCLS].
- Additives to specimen collection tubes can be conveniently studied by drawing a whole blood specimen, then dispensing aliquots into a series of tubes containing the different additives.
Comparative method. We recommend that the interference samples also be analyzed by the comparative method, particularly when the comparative method is a routine service method. If both methods suffer from the same interference, this interference may not be sufficient grounds for rejecting the method. The test method may have other characteristics that would still improve the overall performance of the test. If the reason for changing methods is to get rid of an interference, then, of course, the interference data should be used to reject the new method.
Data calculations
The data analysis is equivalent to calculation of "paired t-test statistics" in a method comparison study and can be carried out with the same statistical program. However, the number of paired samples will be much smaller than the 40 specimens typically required in the comparison of methods study. Note also that "regression statistics" are not appropriate here because the data are not likely to demonstrate a wide analytical range. Here's a step by step procedure for calculating the data:
- Tabulate the results for the pairs of samples.
Sample A I added = 110, 112 mg/dL; Sample A dilution = 98, 102 mg/dL;
Sample B I added = 106, 108 mg/dL; Sample B dilution = 93, 95 mg/dL;
Sample C I added = 94, 98 mg/dL; Sample C dilution = 80, 84 mg/dL; - Calculate the average of the replicates.
Sample A I added = 111 mg/dL; Sample A dilution = 100 mg/dL;
Sample B I added = 107 mg/dL; Sample B dilution = 94 mg/dL;
Sample C I added = 96 mg/dL; Sample C dilution = 82 mg/dL; - Calculate the differences between the results on the paired samples.
Sample A difference = 11 mg/dL
Sample B difference = 13 mg/dL
Sample C difference = 14 mg/dL - Calculate the average the difference for all the specimens tested at a given concentration or level of interference.
Average interference = 12.7 mg/dL
Criterion for acceptable performance
The judgment on acceptability is made by comparing the observed systematic error with the amount of error that is allowable for the test. For example, a glucose test is supposed to be correct to within 10% according to the CLIA proficiency testing criteria for acceptable performance. (See analytical quality requirements.) At the upper end of the reference range (110 mg/dL), the allowable error would be 11.0 mg/dL Because the observed interference of 12.7 mg/dL is greater than the allowable error, the performance of this method is not acceptable.
Recovery Experiment
Recovery studies are a classical technique for validating the performance of an analytical method. However, their use in clinical laboratories has been fraught with problems due to improper performance of the experiment, improper calculation of the data, and improper interpretation of the results. Recovery studies, therefore, are used rather selectively and do not have a high priority when another analytical method is available for comparison purposes. However, they may still be useful to help understand the nature of any bias revealed in the comparison of methods experiment. In the absence of a reliable comparison method, recovery studies should take on more importance.
Purpose
The recovery experiment is performed to estimate proportional systematic error. This is the type of error whose magnitude increases as the concentration of analyte increases. The error is often caused by a substance in the sample matrix that reacts with the sought for analyte and therefore competes with the analytical reagent. The experiment may also be helpful for investigating calibration solutions whose assigned values are used to establish instrument set points.
Factors to consider
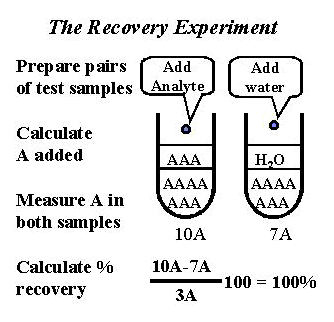 The experimental procedure is outlined in the accompanying figure. Note that pairs of test samples are prepared in a manner similar to the interference experiment. The important difference is that the solution added contains the sought for analyte (shown as A) rather than an interfering material (shown as I in earlier figure). The solution added is often a standard or calibration solution of the sought for analyte. Both test samples are then analyzed by the method of interest.
The experimental procedure is outlined in the accompanying figure. Note that pairs of test samples are prepared in a manner similar to the interference experiment. The important difference is that the solution added contains the sought for analyte (shown as A) rather than an interfering material (shown as I in earlier figure). The solution added is often a standard or calibration solution of the sought for analyte. Both test samples are then analyzed by the method of interest.
Volume of standard added. It is important to keep the volume of standard small relative to the volume of the original patient specimen to minimize the dilution of the original specimen matrix. Otherwise, the error may change as the matix is diluted. We recommend that the dilution of the original specimen be no more than 10%. For a practical procedure, add 0.1 ml of standard solution to 0.9ml or 1.0 ml of patient specimen.
Pipetting accuracy. This is critical because the concentration of analyte added will be calculated from the volume of standard and the volume of the original patient specimen. The experimental work must be carefully performed. High quality pipets should be used and careful attention given to their cleaning, filling, and time for delivery.
Concentration of analyte added. One practical guideline is to add enough of the sought for analyte to reach the next decision level for the test. For example, for glucose specimens with normal reference values in the range of 70 to 110 mg/dL, an addition of 50 mg/dL would raise the concentrations to 120 to 160 mg/dL, which are in the elevated range where medical interpretation of glucose tests will be critical. It is also important to consider the measurement variability of the method. A small level of addition will be more affected by the imprecision of the method additions that a large level of addition.
Concentration of standard solution. Given the importance of adding a small volume to minimize the effect of dilution, it will be desirable to use standard solutions with high concentrations. For our glucose example, a standard solution having 500 mg/dL would be needed to make an addition of 50 mg/dL, assuming 0.1 ml of standard is added to 0.9 ml of a patient specimen. A standard solution of 1,000 mg/dL would be needed to make an addition of 100 mg/dL. The concentration of the standard solution can be calculated once the volumes of the standard addition and the patient specimen are decided. If a general procedure of using 0.1 ml of standard and 0.9 ml of patient specimen is adopted, then the concentration of the standard solution will need to be 10 times the desired level of addition.
Number of replicate measurements per test specimen. Replicate measurements should be made on all test samples because the random error of the measurements often makes it difficult to observe small systematic errors. As a general rule, perform duplicate measurements. If the standard addition is low relative to the concentration of the original specimens, it may be desirable to perform triplicate or quadruplicate measurements.
Number of patient specimens tested. This depends on the competitive reaction that might cause a systematic error. For example, if the concern is to determine whether protein in a serum sample affects the analytical reaction, then only a few patient specimens need be investigated since they all contain protein. If the concern is to determine whether any drug metabolites affect recovery, then specimens from many different patients must be tested.
Verification of experimental technique. It is good practice to analyze the recovery samples by both the test and comparison methods. There are occasional problems caused by instability of the standard solutions, errors in preparation of samples, mixup of test samples, and mistakes in the data calculations. If the comparison method shows the same recovery as the test method, the results of this experiment are of limited value in assessing the acceptability of the test method.
Data calculations
Recovery should be expressed as a percentage because the experimental objective is to estimate proportional systematic error, which is a percentage type of error. Ideal recovery is 100.0%. The difference between 100 and the observed recovery (in percent) is the proportional systematic error. For example, a recovery of 95% corresponds to a proportional error of 5%.
Recovery calculations are tricky and often performed incorrectly, even in studies published in scientific journals. Here's a step-by-step procedure for calculating the data:
- Calculate the amount of analyte added by multiplying the concentration of the standard solution by the dilution factor (ml standard)/(ml standard + ml specimen).
For example, for a calcium method, if 0.1 ml of a 20 mg/dL standard is added to 1.0 ml of serum, the amount added is 20*(0.1/1.1) or 1.82 mg/dL. - Average the results for the replicate measurements on each test sample.
Sample A addition = (11.4 +11.6)/2 = 11.5 mg/dL;
Sample A dilution = (9.7 + 9.9)/2 = 9.8 mg/dL;
Sample B addition = (11.2 + 11.0)/2 = 11.1 mg/dL;
Sample B dilution = (9.5 + 9.5)/2 = 9.5 mg/dL; - Take the difference between the sample with addition and the sample with dilution.
Sample A addition = 11.5, Sample A dilution = 9.8, difference = 1.7 mg/dL
Sample B addition = 11.1, Sample B dilution = 9.5, difference = 1.6 mg/dL - Calculate the recovery for each specimen as the "difference" [step 3] divided by the amount added [step 1].
(1.7 mg/dL/1.82 mg/dL)100 = 93.4% recovery
(1.6 mg/dL/1.82 mg/dL)100 = 87.9% recovery
[Note the variability of these estimates, which is likely due to the imprecision of the method; it may actually be desirable to perform more replicate measurements or prepare more test samples.] - Average the recoveries from all the specimens tested.
(93.4 + 87.9)/2 = 90.6% average recovery - Calculate the proportional error.
100 - 90.6 = 9.4% proportional error
Criterion for acceptable performance
The observed error is compared to the amount of error allowable for the test. For calcium, for example, the CLIA criterion for acceptable performance is 1 mg/dL. At the middle of the reference range, about 10 mg/dL, the allowable total error is 10%. Given that the observed proportional error is 9.4%, performance just meets the CLIA criterion for acceptability.
Summary Comments
Interference and recovery experiments can be used to assess the systematic errors of a method. They complement the comparison of methods experiment by allowing quick initial estimates of specific errors - the interference experiment for constant systematic error and the recovery experiment for proportional systematic error. In the absence of a comparison method, they provide an alternative way of estimating systematic errors.
- The experimental techniques are similar, but the material being added is different. A suspected interfering material is added in the interference experiment, whereas the sought for analyte is added in the recovery experiment.
- The data calculations are different. The bias between paired samples should be calculated for the interference data, in a manner similar to the calculation of t-test statistics in the comparison of methods experiment. The average recovery in percent should be calculated from the recovery experiment, being careful to divide the difference between paired samples by the amount added, not by the total after addition. The proportional systematic error is the difference between 100% and the observed % recovery.
- Interference experiments are generally useful to test the effects of common sample conditions, such as high bilirubin, hemolysis, lipemia, and additives to specimen collection tubes. Results in the literature are generally reliable.
- Recovery studies are performed less frequently and results in the literature are difficult to interpret due to the lack of a standard way of calculating the data. A great deal of care and attention is necessary when performing recovery studies and also when interpreting the results.
- When making judgments on method performance, the observed errors should be compared to the defined allowable error. The bias estimate from an interference experiment can be compared directly to an analytical quality requirement expressed in concentration units. The average recovery needs to be converted to proportional error (100 - %Recovery) and then compared to an analytical quality requirement expressed in percent.
References
- Katz SM, DiSalvio TV. Ascorbic acid effects on serum glucose values. JAMA 1973;224:628.
- Young DS. Effects of preanalytical variables on clinical laboratory tests. Washington DC:AACC Press, 1993.
- NCCLS Document EP7-P. Interference testing in clinical chemistry. Wayne, PA:NCCLS, 1986.

