Quality of Laboratory Testing
Part I: Myths and Metrics
- Myths of Laboratory Quality
- Metrics for Laboratory Quality
- Example using the DPM methodology
- Example using process performance characteristics
- What are the Sigma metrics for your laboratory methods?
- What is the quality of laboratory testing today?
- References
September 2004
with Sten Westgard, MS
Are the laboratory Quality Control problems that were experienced at Maryland General Hospital indicative of a few bad apples or a systemic problem? For background on this issue, see earlier discussions on this website:- Part I. Cracks
- Part II. Facts
- Part III. Broken Windows
- Part IV. Inadequate Inspections
- Part V. A few bad apples or the tip of the iceberg?
Based on the congressional hearings, it appears that CMS and FDA see no need for major changes in the regulatory rules and process, only a few minor changes to provide better communication of inspection results. They have concluded that the MGH problem is the result of a “few bad apples”.
CAP also favors the “few bad apples” theory. According to Ron Lepoff, MD, FCAP, Chair of the CAP Commission on Laboratory Accreditation, “I’ve been doing inspections since l974, and I’ve seen a lot of laboratories in that time. In my experience, what happened at Maryland General is an aberration.” [1]
Other professional organizations also seem to accept the bad apple theory. None have come forward to advocate changes in the regulatory rules and process.
Is it really safe to conclude that the quality of laboratory tests is okay? CMS’s own inspection results show from 5% to 10% of laboratories are cited for deficiencies related to QC. And given that high a level of deficiencies, CMS is moving forward to change the QC requirements to allow laboratories to reduce QC from 2 levels per day to 2 levels per week or even 2 levels per month for instruments having internal procedural controls, e.g., electronic QC. Is that going to make laboratory testing more or less safe?
Myths of laboratory quality
It is widely believed that the quality of laboratory testing is better than needed for medical care! How else can you explain the ongoing reduction in laboratory QC in spite of the documented deficiencies of current laboratory QC practices? CMS and FDA clearly believe this to be true, otherwise they would respond to the MGH problem with corrective actions. Professional organizations, such as CAP and JCAHO, obviously believe this to be true when they defend the adequacy of their inspection practices and procedures. Other professional organizations, such as AACC, ASCP, and CLMA, must believe this to be true since they show no interest in coming forward to advocate changes in the status quo.In the absence of concrete evidence, this belief should more properly be labeled a myth, i.e., a “Mistaken Yearning, Theory, or Hypothesis.” How can we be sure that laboratory quality is better than needed for medical care when few laboratories even know what quality is needed? How do you define the quality that is needed for the tests performed in your laboratory? Where is the data to show that your performance is better than the defined medical needs?
A corollary to this myth is the belief that manufacturers assure the necessary quality when they obtain FDA approval for new laboratory systems, instruments, and methods! But, manufacturers DON’T make any claims for quality when they obtain FDA approval to market new analytical systems. They do make claims for precision and accuracy, but they DON’T compare those claims with any stated requirements for test performance or medical quality, nor do they ever define the medical quality that is needed anywhere in the product performance claims.
Another corollary is that the government, through the CLIA regulations, assures that laboratory quality is good enough for medical care. The belief that running 2 controls per day or week or month is sufficient to assure or guarantee the necessary quality has no scientific basis. Can all methods – manual and automated, simple and complex, performed by highly and lowly skilled analysts - be adequately controlled with 2 levels per day or week or month? Can it be that simple?
Metrics for laboratory quality
Six Sigma quality management has introduced a standard metric, called the Sigma-metric, as a universal measure of quality. Sigma represents the observed variation of a product or process, e.g., the standard deviation of an analytical testing process. The Sigma metric indicates the number of sigmas that fall within the “tolerance specifications” or quality requirement of the product or process (such as the allowable total error for a laboratory test). The higher the value of the Sigma metric, the better the product or process. A sigma value of 3 is generally considered the minimal acceptable quality for a product or process and a value of 6 Sigma is considered the goal for world class quality.Fundamental to the determination of the Sigma etric is the need to define what constitutes a defective product or a defective test result. To apply this approach for quality assessment of laboratory processes, there are two methodologies that are useful:
- For pre-analytic and post-analytic processes, count the number of defects in a group, calculate the defects per million (DPM), then utilize a standard table to convert DPM to the sigma value.
- For analytic processes whose performance characteristics are known, i.e., whose precision (s) and accuracy (bias) can be estimated directly from experimental data, define the “tolerance limit” in the form of an allowable total error, TEa, such as specified in the CLIA proficiency testing criteria for acceptable performance, and calculate the sigma from the following equation:
Example using the DPM methodology
Let’s take the Maryland General Hospital numbers for the retest results on HIV and hepatitis C patients. During a 14-month period, from June 2002 to August 2003, some 2,169 patients were tested and may have received incorrect test results. Of the over one thousand who were retested, “99.4% of HIV test results have been reconfirmed to be consistent with the original tests,” according to the testimony from Edmond F. Notebaert at the Congressional hearings July 7, 2004 [2].- Step 1. Determine the “defects per million” (DPM). A 99.4% yield of correct test results indicates that the defect rate is 0.6%, which is the same as 6,000 DPM.
- Step 2. Convert DPM to sigma using a standard conversion table that shows DPM vs Sigma values. Using the conversion table on this website, find 6000 DPM in column 1. Read the corresponding Sigma in column 2 “short-term” and column 3 “long term”. Those metrics should be 4.0 and 2.5, respectively.
The usual convention is to use the “short-term” figure when making the DPM conversion from the table. This Sigma metric of 4.0 seems like an acceptable level of quality unless you are one of the patients who got a wrong test result! Being labeled HIV positive can have significant impact on your life, as evidenced by one patient’s story from the MGH case [3]. That’s why it’s desirable to aim for a very low defect rate, or 6-Sigma performance, when the cost of false test results has profound impact on the lives of our patients.
Example using process performance characteristics
The second methodology is particularly applicable to analytical testing processes where performance characteristics, such as precision and accuracy, can be directly estimated from experimental data. Rather than trying to inspect test results and determine which are defective, this methodology predicts the number of defects that will occur on the basis of the known variation of the process. Here’s how it works.- Step 1. Define the tolerance limits, e.g., start with the CLIA criteria for acceptable performance that describe TEa, the total error that is allowable in test results.
- Step 2. Estimate method imprecision (s) from the replication experiment performed in the initial validation studies, or from QC data collected in routine operation.
- Step 3. Estimate method inaccuracy (bias) from the comparison of methods experiment performed in the initial method validation studies, or from proficiency testing data or peer comparison data collected in routine operation.
- Step 4. Calculate the Sigma metric from the formula Sigma = [(TEa-bias)/s].
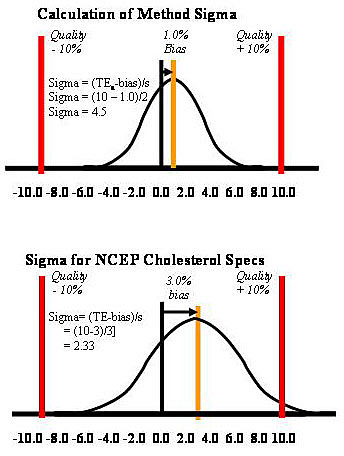 Taking cholesterol as an example, the CLIA criterion for acceptable performance is 10%. Given a method whose imprecision is 2.0% (s expressed in %, or CV) and whose bias is 1.0%, the sigma-metric would be 4.5 [(10-1)/2]. This application is described graphically at the top part of the accompanying figure. The tolerance limits are shown by the vertical lines at plus and minus 10%. The bias is shown by the 1% displacement of the mean of the test distribution from the middle of the scale. The distribution itself shows the sizes of errors that are expected due to the method’s observed imprecision, or s. For comparison, a cholesterol method that just meets the specifications of the National Cholesterol Education Program (NCEP) for a maximum CV of 3% and a maximum bias of 3.0% would have 2.33 Sigma performance [(10-3)/3]. With this method, ideal performance under stable conditions generates a considerable number of defective test results. In other industries, such performance would not be considered acceptable for routine use.
Taking cholesterol as an example, the CLIA criterion for acceptable performance is 10%. Given a method whose imprecision is 2.0% (s expressed in %, or CV) and whose bias is 1.0%, the sigma-metric would be 4.5 [(10-1)/2]. This application is described graphically at the top part of the accompanying figure. The tolerance limits are shown by the vertical lines at plus and minus 10%. The bias is shown by the 1% displacement of the mean of the test distribution from the middle of the scale. The distribution itself shows the sizes of errors that are expected due to the method’s observed imprecision, or s. For comparison, a cholesterol method that just meets the specifications of the National Cholesterol Education Program (NCEP) for a maximum CV of 3% and a maximum bias of 3.0% would have 2.33 Sigma performance [(10-3)/3]. With this method, ideal performance under stable conditions generates a considerable number of defective test results. In other industries, such performance would not be considered acceptable for routine use.
What are the Sigma metrics for your laboratory methods?
You can figure them out from the CLIA criteria and performance data available in your laboratory. You have the necessary data. The calculations are simple. As a starting point, take the CLIA table that identifies individual tests and their criteria for acceptable performance. Do the following:- Set up an electronic spreadsheet with the following columns: Test, TEa %, QC mean, QC s % or CV, bias %, and sigma [where Sigma = (TEa% – bias%)/CV%). Note that all these numbers must have common units, either concentration units or percentage unit.
- Fill in the test and TEa values from the CLIA table.
- Fill in the mean and CV values for results of a particular control material that has been analyzed for that test and method. That estimate could come from the replication experiment in the initial method validation studies. Or, it could be made using routine QC data, in which case the results from a one month period should be included.
- Enter 0.0 in the bias column in your initial assessment. This will cause the Sigma values to be too high, i.e., they will be optimistic estimates. Just keep that in mind when you look at the resulting Sigma values.
- Review the Sigmas for the different tests. Remember, these estimates will be on the high side because method bias has been assumed to be zero.
What is the quality of laboratory testing today?
This, of course, is the question that needs to be answered to know whether the Maryland General incident is indicative of a few bad apples or a more widespread systemic problem.We intend to investigate this issue in the next reports in this series. This will involve making use of data from proficiency testing reports that are available to the public, as well as peer-comparison reports. We will also solicit input of government agencies, professional organizations, and business services that have access to data on current laboratory performance.
References
-
Parham S. Hearings Investigate Cause of Invalid HIV, HCV Results. Clin Lab News, 2004:30 (Number 6, August).
-
Notebaert EF. Testimony before the House Government Reform Subcommittee on Criminal Justice, Drug Policy and Human Resources regarding Maryland General Hospital, July 7, 2004.
-
Julie Bell. “Patient sues over HIV test mistake.” Baltimore Sun, August 13, 2004.
James O. Westgard, PhD, is a professor of pathology and laboratory medicine at the University of Wisconsin Medical School, Madison. He also is president of Westgard QC, Inc., (Madison, Wis.) which provides tools, technology, and training for laboratory quality management.
