Six Sigma
Six Sigma and Requisite Laboratory QC
In the healthcare market, a lot of manufacturers are issuing products with more of an eye on their profit margin than on the quality of the product. If your manufacturer can't meet Six Sigma requirements, what can you do? Improve your internal laboratory QC -- Dr. Westgard explains how. (preview)
- QC performance characteristics
- A sigma-metric for QC design
- Complementary process and QC capabilities
- Graphical assessment of process capability
- Graphical matching of QC error detection to process capability
- Design and planning tools for six-sigma quality management
- References
In the previous essay, I described the implications of Six Sigma Quality Management for setting analytical specifications for the precision and bias of laboratory testing processes [1]. The desirable precision is 1/6 of the tolerance specification or 1/6 of the allowable total error for a laboratory test. One way of applying this to laboratory tests is to divide the CLIA proficiency testing acceptability criteria by 6 to establish specifications for the precision of laboratory methods [see the table in the previous discussion, 1]. When this precision performance is achieved, the Six Sigma model postulates that a bias up to 1.5 times the standard deviation of the method should be tolerable without causing defective results. Larger biases that would cause significant defects should be readily detectable by simple statistical QC procedures, such as use of 3 SD control limits with a very low number of control measurements.
BUT, what should you do if your method doesn't achieve six-sigma performance? Of course, the first option is to improve method performance, but that often depends on the cooperation of the manufacturer. Today's highly automated systems may not allow you to make any process improvements on your own. The other option is to beef up the statistical QC procedure so you can detect smaller changes, reject runs having defects, and perform corrective actions to prevent further defects. You still have control of your laboratory QC procedure and can select control rules and numbers of control measurements to assure the quality needed by your laboratory.
QC performance characteristics
Different QC procedures (e.g., different control rules and different numbers of control measurements) have different sensitivities or capabilities for detecting analytical errors. The accompanying graph, called a power function graph, shows the rejection characteristics or power curves for QC procedures that are commonly used in clinical laboratories [2]. The control rules and number of control measurements are given in the key at the right, where the lines, top to bottom, correspond with the curves on the graph, top to bottom. All these QC procedures are for two control measurements (N=2), but with different control rules. The top line is for a 12s control rule, which corresponds to a Levey-Jennings control chart having limits calculated as the mean plus and minus 2 SD. The middle line corresponds to a multirule procedure that employs three different control rules - 13s/22s/R4s. The other lines are single rule procedures with control limits of 2.5s, 3.0s, and 3.5s.
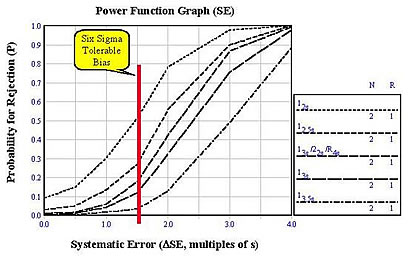
The y-axis gives the probability of rejection from 0 to 1.0 and the x-axis gives the size of a systematic error in multiples of the method standard deviation (s). The probability for an x-value of 0.0 describes the probability for false rejection. The probability for an x-value of 1.5 describes the probability of detecting a systematic shift equivalent to 1.5 times the method standard deviation. For example, if the tolerance or quality requirement were 12% and the method has a CV of 2% (6-Sigma performance), then a systematic error of 3% or 1.5s corresponds to the tolerable bias in the six sigma model. A QC procedure having 2 control measurements and control limits set at 3s would have a probability of false rejection of almost 0.00 and a probability of about 0.12, or a 12% chance, of rejecting a production run having a systematic shift or error equivalent to 1.5s.
 Want to read more of this article?
Want to read more of this article?
We invite you to purchase the Six Sigma QC Design and Control manual, Second Edition, available at our online store. You can also download the Table of Contents and a Sample chapter.
