Break all the rules (Part 3)

After a significant time elapsed since parts one and two, we continue our series on basic QC interpretation. We are finally tackilng that most complex scenario: what happens when we have 3 controls? How do we interpret across materials/levels? Does that mean we stop interpreting across runs? Here's another simple exercise - if you're told that all the rules have been broken, can you find where the violations occurred?

Break All the Rules! (Part Three)

Sten Westgard, MS
July 2017

As laboratorians, we are constantly pressured to achieve compliance, to operate with an absence of problems, to generate a stream of data points that land lovingly near the mean. As a contrarian exercise, this article is about the exact opposite of getting all your data to stay in control. We're going to look at data that's out-of-control, breaking all of the various "Westgard Rules." And we're going to see if you can identify which data points are outliers and which rules are being broken.

As the title suggests, this is third installment. Part One was just one control. Part Two was two controls. Now we're going to get about as complicated as most labs gets. We're going to look at rule violations with three controls.

The data

The following data set is going to have a low control with a mean of 47 and an SD of 3 and a middle control with a mean of 71 and an SD of 8 and a high control of 256 with an SD of 18. I'm not going to tell you which test or what units are involved. They're irrelevant to this exercise. We're also not going to look at the total allowable error or CV or bias. All of that becomes important after we know the basics of QC and charting.

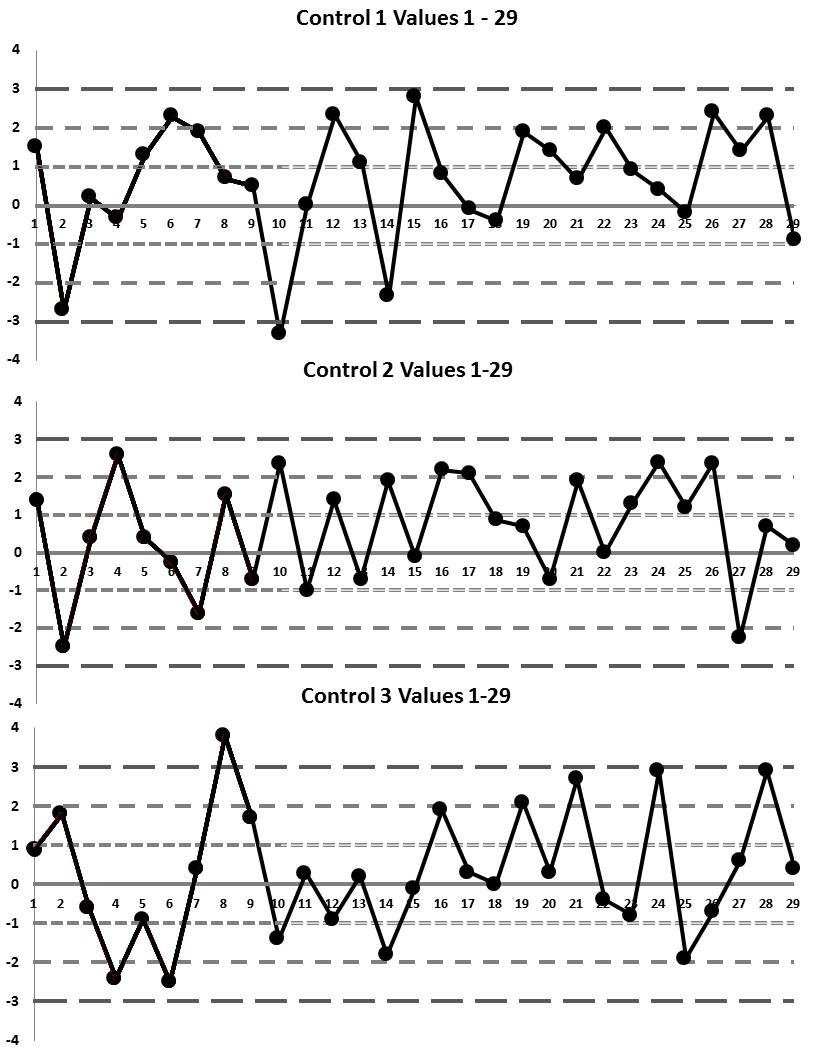
To make it a little easier to understand this data, here are the Levey-Jennings charts for these first 29 values (notice for each control, not only is the raw value given, but the z-score is shown as well - that's really useful):

Values	Control 1	1-z	Control 2	2-z	Control 3	3 -z	RULE BROKEN?
Run 1	51.5	1.5	82.2	1.4	272.2	0.9
Run 2	38.9	-2.7	51	-2.5	288.4	1.8
Run 3	47.6	0.2	74.2	0.4	245.2	-0.6
Run 4	46	-0.33333	91.8	2.6	212.8	-2.4
Run 5	50.9	1.3	74.2	0.4	239.8	-0.9
Run 6	53.9	2.3	69	-0.25	211	-2.5
Run 7	52.7	1.9	58.2	-1.6	263.2	0.4
Run 8	49.1	0.7	83.3	1.54	324.4	3.8
Run 9	48.5	0.5	65.4	-0.7	286.6	1.7
Run 10	37	-3.33	90	2.375	230.8	-1.4
Run 11	47	0	63	-1	261.0	0.28
Run 12	54	2.333333	82.2	1.4	239.8	-0.9
Run 13	50.3	1.1	65.4	-0.7	259.6	0.2
Run 14	40	-2.33333	86.2	1.9	223.6	-1.8
Run 15	55.4	2.8	70.2	-0.1	254.2	-0.1
Run 16	49.4	0.8	88.6	2.2	290.2	1.9
Run 17	46.7	-0.1	87.8	2.1	261.4	0.3
Run 18	45.8	-0.4	78	0.875	256.0	0.0
Run 19	52.7	1.9	76.6	0.7	293.8	2.1
Run 20	51.2	1.4	65.4	-0.7	261.4	0.3
Run 21	49	0.667	86.2	1.9	304.6	2.7
Run 22	53	2	71	0	248.8	-0.4
Run 23	49.7	0.9	81.4	1.3	241.6	-0.8
Run 24	48.2	0.4	90.2	2.4	308.2	2.9
Run 25	46.4	-0.2	80.6	1.2	221.8	-1.9
Run 26	54.2	2.4	90	2.375	243.4	-0.7
Run 27	51.2	1.4	53	-2.25	266.8	0.6
Run 28	53.9	2.3	76.6	0.7	308.2	2.9
Run 29	44.3	-0.9	72.6	0.2	263.2	0.4

If the table is too hard to work with, here are the three Levey-Jennings charts (click on the graph to enlarge the figures):

Here is the second table of QC values for runs 30 through 59:

Values	Control 1	1-z	Control 2	2-z	Control 3	3-z	Rule Broken?
30	48.5	0.5	84.6	1.7	279.4	1.3
31	48.8	0.6	79.8	1.1	254.2	-0.1
32	46.7	-0.1	82.2	1.4	250.6	-0.3
33	46.1	-0.3	83.8	1.6	265	0.5
34	49.7	0.9	72.6	0.2	279.4	1.3
35	53.9	2.3	63.8	-0.9	286.6	1.7
36	52.1	1.7	60.6	-1.3	284.8	1.6
37	48.2	0.4	62.2	-1.1	245.8	-0.6
38	52.1	1.7	71	0	286.6	1.7
39	50.6	1.2	69.4	-0.2	261.4	0.3
40	50.3	1.1	64.6	-0.8	245.2	-0.6
41	44.3	-0.9	87.8	2.1	263.2	0.4
42	51.8	1.6	79.8	1.1	281.2	1.4
43	41.9	-1.7	64.6	-0.8	284.8	1.6
44	49.4	0.8	63.8	-0.9	261.4	0.3
45	48.8	0.6	75.8	0.6	241.6	-0.8
46	49.9	0.97	66.2	-0.6	263.2	0.4
47	52.4	1.8	71	0	293.8	2.1
48	52.7	1.9	82.2	1.4	248.8	-0.4
49	49.1	0.7	56.6	-1.8	223.6	-1.8
50	44	-1	66.2	-0.6	229	-1.5
51	48.8	0.6	82.2	1.4	247	-0.5
52	50.6	1.2	77.4	0.8	266.8	0.6
53	43.7	-1.1	78.2	0.9	290.2	1.9
54	47.6	0.2	75	0.5	281.2	1.4
55	45.5	-0.5	85.4	1.8	245.2	-0.6
56	44.3	-0.9	86.2	1.9	261.4	0.3
57	52.4	1.8	55.8	-1.9	221.8	-1.9
58	53.9	2.3	65.4	-0.7	277.6	1.2
59	45.2	-0.6	83.8	1.6	284.8	1.6

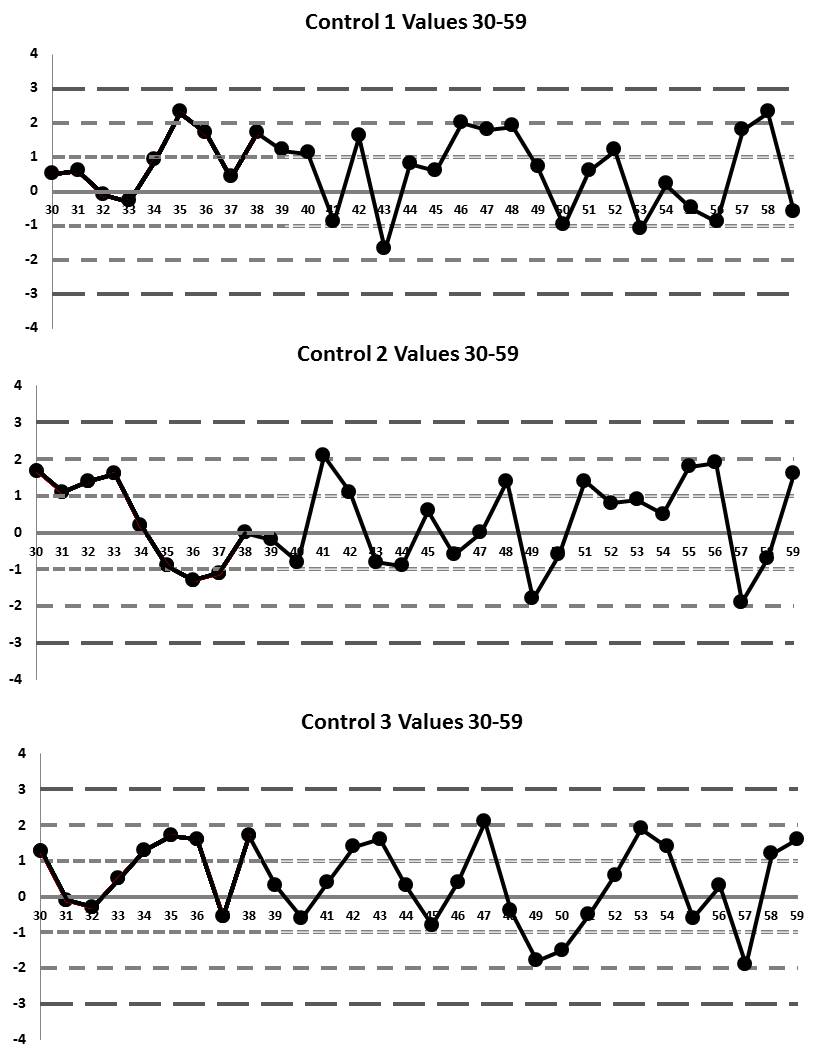
And now the Levey-Jennings charts for runs 3 through 59:

2017 break all the rules N=3 runs 30 through 59

Next, we're ready to see the table of data for runs 60 through 89:

Values	Control 1	z 1	Control 2	Z 2	Control 3	z 3	Rule Broken?
60	45.8	-0.4	74.2	0.4	277.6	1.2
61	50.6	1.2	64.6	-0.8	284.8	1.6
62	48	0.3	83	1.5	266.8	0.6
63	49	0.7	83	1.5	259.6	0.2
64	46	-0.3	67.1	-0.49	260.1	0.23
65	53	2.0	74.2	0.4	281.2	1.4
66	48	0.3	80.6	1.2	241.6	-0.8
67	45.8	-0.4	71.8	0.1	272.2	0.9
68	48.2	0.4	69.4	-0.2	288.4	1.8
69	50.9	1.3	81.4	1.3	250.6	-0.3
70	48.2	0.4	65.4	-0.7	277.6	1.2
71	51.2	1.4	70	-0.125	221.8	-1.9
72	49.1	0.7	69	-0.25	263.2	0.4
73	51.5	1.5	66	-0.625	247	-0.5
74	47.9	0.3	68.6	-0.3	254.2	-0.1
75	48.5	0.5	86.2	1.9	261.4	0.3
76	50.9	1.3	59.8	-1.4	266.8	0.6
77	46.7	-0.1	67.8	-0.4	252.4	-0.2
78	47.8	0.3	86.2	1.9	236.2	-1.1
79	45.5	-0.5	72.6	0.2	250.6	-0.3
80	52	1.7	81.4	1.3	259.6	0.2
81	52	1.7	74.2	0.4	243.4	-0.7
82	48.5	0.5	80.6	1.2	275.8	1.1
83	44.3	-0.9	79.8	1.1	281.2	1.4
84	49.4	0.8	75	0.5	252.4	-0.2
85	46.7	-0.1	76.6	0.7	272.2	0.9
86	52.7	1.9	72.6	0.2	281.2	1.4
87	45.2	-0.6	55.8	-1.9	275.8	1.1
88	48.8	0.6	79	1	256	0
89	46.4	-0.2	70.2	-0.1	236.2	-1.1

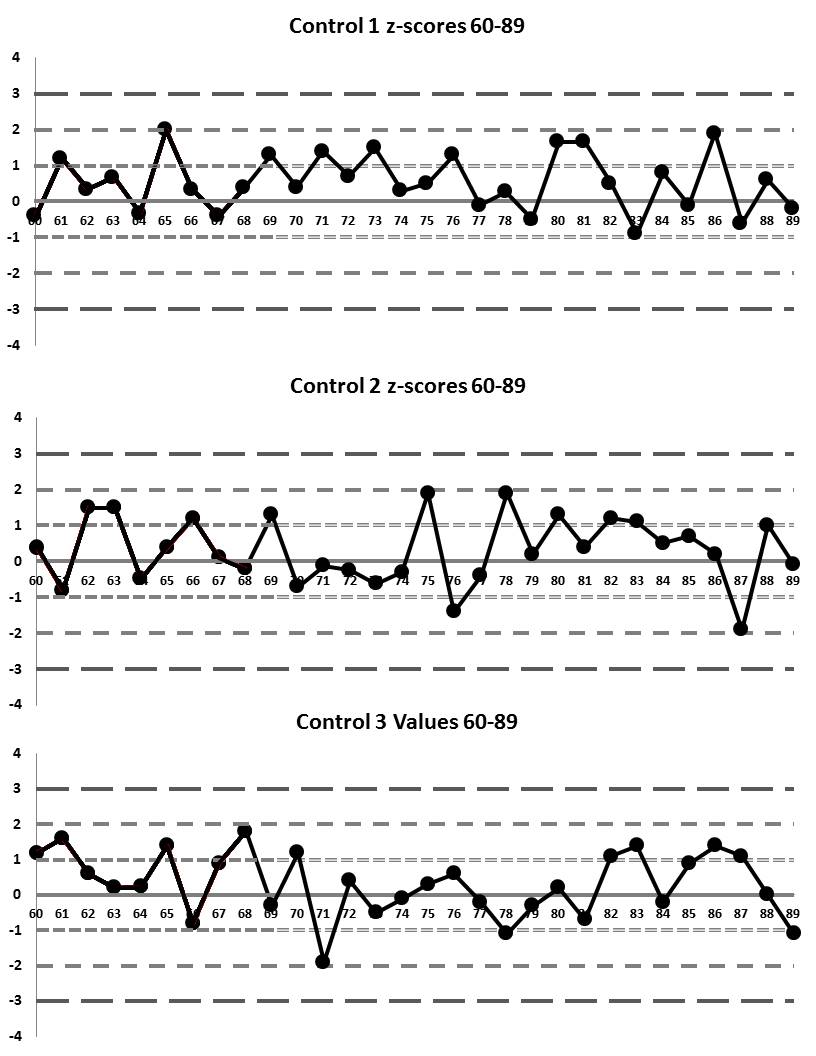
Now there are some Levey-Jennings charts for those runs 60 through 89:

Break All The Rules N3 runs 60 through 89

Now the data table for runs 90 through 119:

Values	Control 1	Z 1	Control 2	Z 2	Control 3	Z 3	Rules
90	49.7	0.9	82.2	1.4	275.8	1.1
91	47	0	68.6	-0.3	265	0.5
92	45.5	-0.5	60.6	-1.3	272.2	0.9
93	46.4	-0.2	79	1	283	1.5
94	51.5	1.5	59.8	-1.4	288.4	1.8
95	48.8	0.6	66.2	-0.6	259.6	0.2
96	44.9	-0.7	77.4	0.8	274	1
97	50.3	1.1	74.2	0.4	281.2	1.4
98	44.3	-0.9	65.4	-0.7	265	0.5
99	46.7	-0.1	63	-1	245.2	-0.6
100	50.6	1.2	74.2	0.4	268.6	0.7
101	49.4	0.8	85.4	1.8	279.4	1.3
102	47.6	0.2	80.6	1.2	288.4	1.8
103	46.7	-0.1	60.6	-1.3	234.4	-1.2
104	50	1	71	0	275.8	1.1
105	51.8	1.6	72.6	0.2	275.8	1.1
106	47.6	0.2	70.2	-0.1	250.6	-0.3
107	50	1	68.6	-0.3	261.4	0.3
108	49.1	0.7	81.4	1.3	230.8	-1.4
109	50.3	1.1	78.2	0.9	232.6	-1.3
110	48.8	0.6	69.4	-0.2	265	0.5
111	51.8	1.6	63	-1	256	0
112	50.6	1.2	82.2	1.4	252.4	-0.2
113	47.3	0.1	80.6	1.2	238	-1
114	48.8	0.6	76.6	0.7	230.8	-1.4
115	47.8	0.3	62.2	-1.1	239.8	-0.9
116	47	0	75	0.5	234.4	-1.2
117	47.6	0.2	81.4	1.3	275.8	1.1
118	46.7	-0.1	83.8	1.6	268.6	0.7
119	44.9	-0.7	72.6	0.2	236.2	-1.1

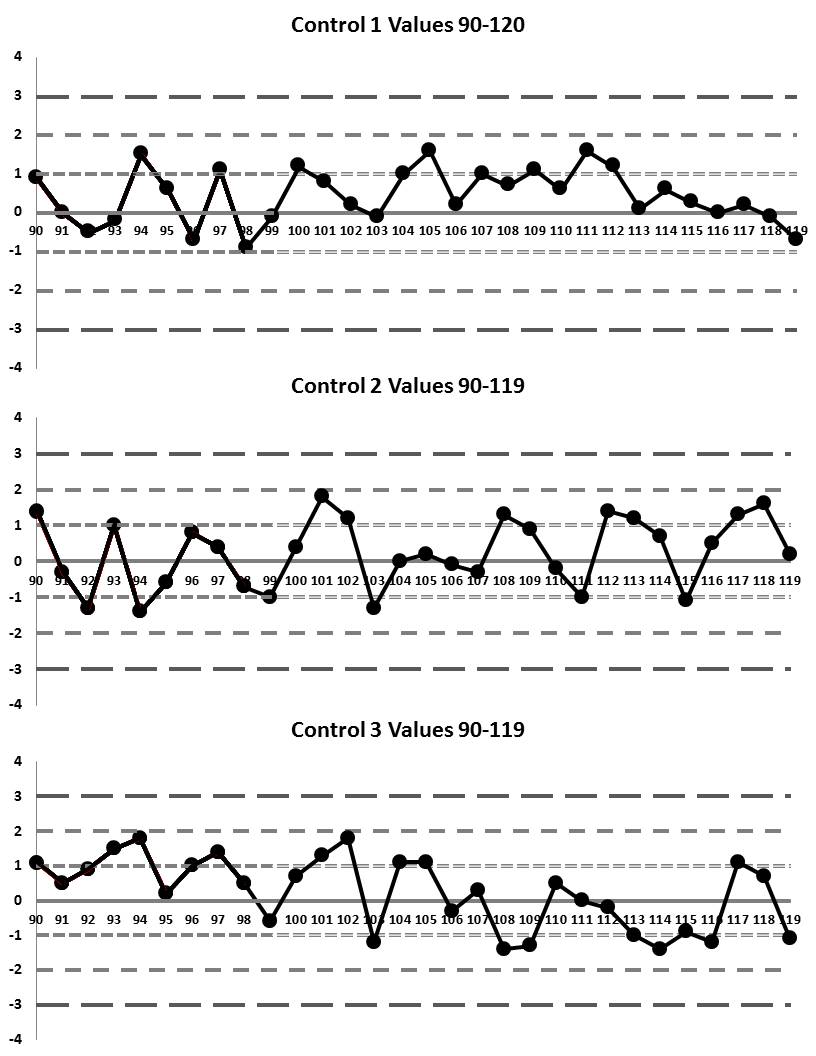
Break All The Rules N3 runs 90 through 120

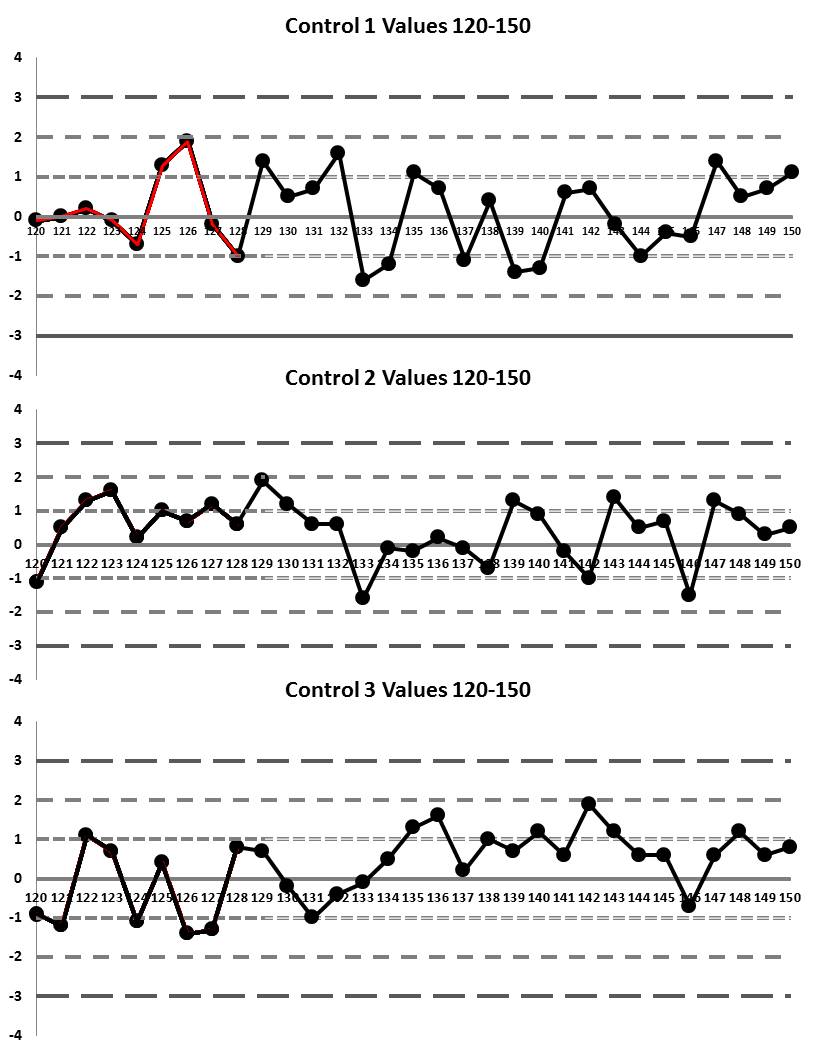
Here's our final table of data, with values 120 through 150. We're just looking for the 12:x violation now:

Values	Control 1	Z 1	Control 2	Z 2	Control 3	Z 3	Rules Broken?
120	46.7	-0.1	62.2	-1.1	239.8	-0.9
121	47	0	75	0.5	234.4	-1.2
122	47.6	0.2	81.4	1.3	275.8	1.1
123	46.7	-0.1	83.8	1.6	268.6	0.7
124	44.9	-0.7	72.6	0.2	236.2	-1.1
125	50.9	1.3	79	1	263.2	0.4
126	52.7	1.9	76.6	0.7	230.8	-1.4
127	46.4	-0.2	80.6	1.2	232.6	-1.3
128	44	-1	75.8	0.6	270.4	0.8
129	51.2	1.4	86.2	1.9	268.6	0.7
130	48.5	0.5	80.6	1.2	252.4	-0.2
131	49.1	0.7	75.8	0.6	238	-1
132	51.8	1.6	75.8	0.6	248.8	-0.4
133	42.2	-1.6	58.2	-1.6	254.2	-0.1
134	43.4	-1.2	70.2	-0.1	265	0.5
135	50.3	1.1	69.4	-0.2	279.4	1.3
136	49.1	0.7	72.6	0.2	284.8	1.6
137	43.7	-1.1	70.2	-0.1	259.6	0.2
138	48.2	0.4	65.4	-0.7	274	1
139	42.8	-1.4	81.4	1.3	268.6	0.7
140	43.1	-1.3	78.2	0.9	277.6	1.2
141	48.8	0.6	69.4	-0.2	266.8	0.6
142	49.1	0.7	63	-1	290.2	1.9
143	46.4	-0.2	82.2	1.4	277.6	1.2
144	44	-1	75	0.5	266.8	0.6
145	45.8	-0.4	76.6	0.7	266.8	0.6
146	45.5	-0.5	59	-1.5	243.4	-0.7
147	51.2	1.4	81.4	1.3	266.8	0.6
148	48.5	0.5	78.2	0.9	277.6	1.2
149	49.1	0.7	73.4	0.3	266.8	0.6
150	50.3	1.1	75	0.5	270.4	0.8

Here are our last graphs of those runs:

2017 break all the rules N=3 runs 120 through 150

That should be enough data to keep you out of trouble. And the number of outliers you find in this dataset should be equivalent to a year's worth of outliers that you see normally in your own lab data.

Finally, I'm going to add the following conditions:

We are running THREE controls per run; assume each trio of values represents one run
We're NOT going to look for 2s violations. Let's break that habit right now. In any case, I didn't generate these data points randomly, so we should not expect to see a certain number of "natural false rejections" in the form of 2s outliers
We ARE going to try to find outliers of the following "Westgard Rules": 1:3s/2of3:2s/R:4s/3:1s/6:x (and later in the exercise, we switch to 9:x and12:x)
We're NOT going to sink into the swamp that is the repeating of controls. So don't assume anything you see is a repeated control - just stick with "in" or "out"

So, at the end of this, can you answer the following questions?

How many rule violations were there?
Which rules were violated and how many times?
What would be different if I told you that only the "Westgard Rules" 1:3s/2of3:2s/R:4s were necessary?
What would be different if I told you that only the 1:3s control rule was necessary?

These answers, and more, in a few weeks...

[Don't submit this exercise for grading. You'll get to compare your answers to the answer set in a few weeks. But feel free to share this with your colleagues and see if you can all reach the same conclusions and interpretations.]

Tools, Technologies and Training for Healthcare Laboratories

Basic QC Practices