Break All the Rules - Answers to Part One

Answers to the Part One (N=1) of Break All The Rules.

Break All the Rules! (Answers to Part One)

Sten Westgard, MS
August 2015

The answers

The following data set is going to have a mean of 47 and an SD of 3. I'm not going to tell you which test or what units are involved. They're irrelevant to this exercise. We're also not going to look at the total allowable error or CV or bias. All of that becomes important after we know the basics of QC and charting.

To make it easier, we transformed the data into z-scores, which tell you how many SDs the point is from the mean, and in what direction. For example, a 42.5 is 42.5-47 = -4.5, which is (-4.5)/3 = -1.5 SDs below the mean. so the z-value of 42.5 is -1.5.

Control Measurement	Value	Z-value	Rule Broken
1	42.5	-1.5
2	55.1	2.7
3	46.4	-0.2
4	47.0	0
5	43.1	-1.3
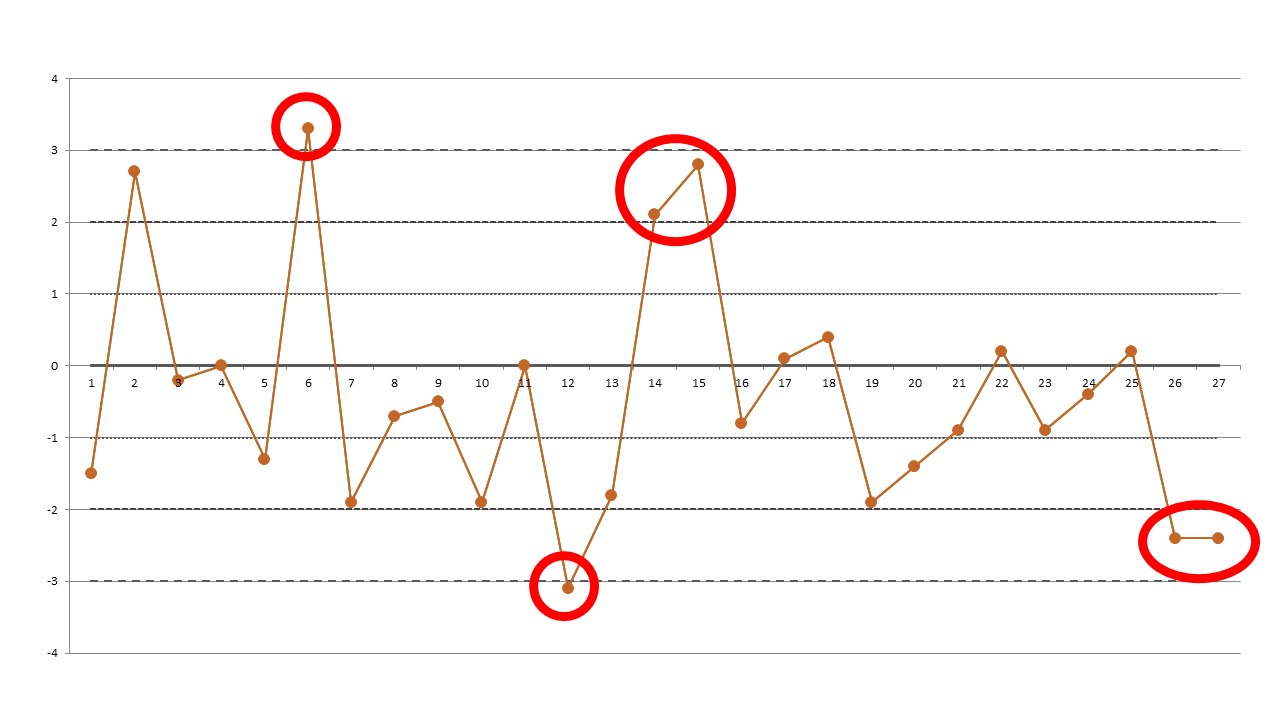
6	56.9	3.3	1:3s rule
7	41.3	-1.9
8	44.9	-0.7
9	45.5	-0.5
10	41.3	-1.9
11	47.0	0
12	37.7	-3.1	1:3s rule
13	41.6	-1.8
14	53.3	2.1	2:2 rule
15	55.4	2.8	2:2 rule
16	44.6	-0.8
17	47.3	0.1
18	48.2	0.4
19	41.3	-1.9
20	42.8	-1.4
21	44.3	-0.9
22	47.6	0.2
23	44.3	-0.9
24	45.8	-0.4
25	47.6	0.2
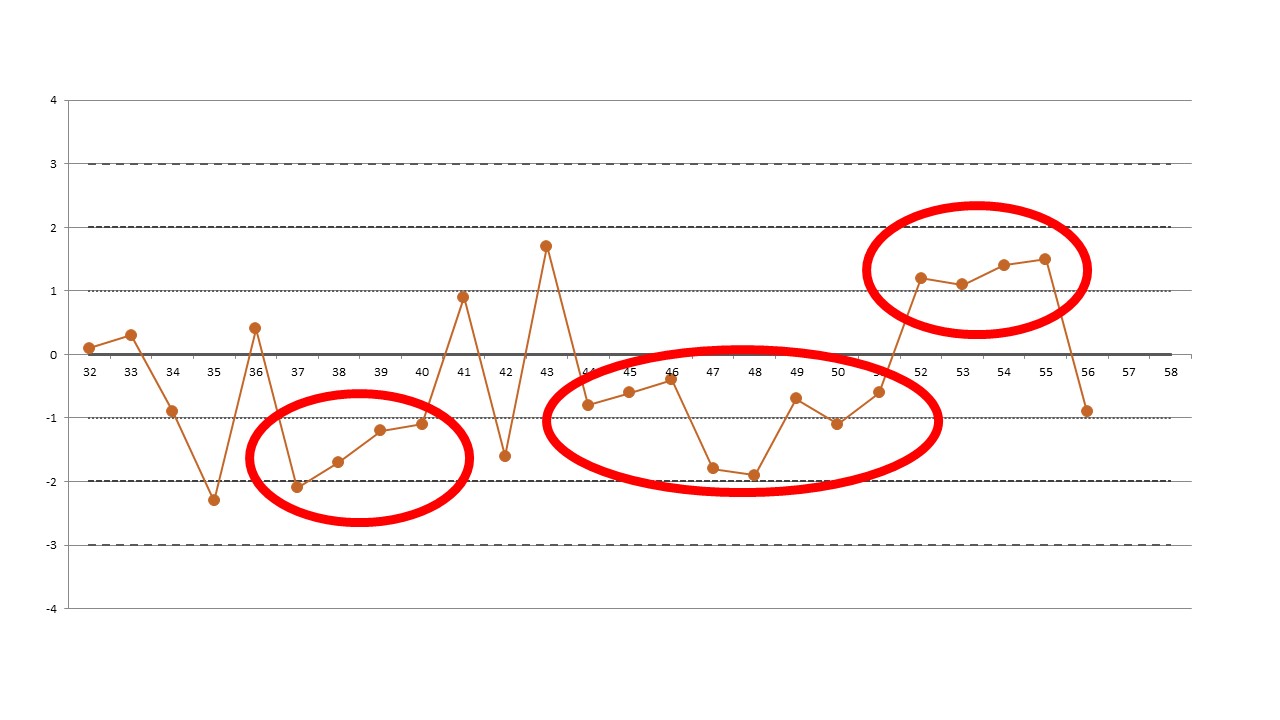
26	39.8	-2.4	2:2s rule
27	39.8	-2.4	2:2s rule
28	50.9	1.3
29	49.7	0.9
30	45.5	-0.5
31	45.2	-0.6
32	47.3	0.1
33	47.9	0.3
34	44.3	-0.9
35	40.1	-2.3
36	48.2	0.4
37	40.7	-2.1	4:1s rule
38	41.9	-1.7
39	43.4	-1.2
40	43.7	-1.1
41	49.7	0.9
42	42.2	-1.6
43	52.1	1.7
44	44.6	-0.8	8:x rule
45	45.2	-0.6
46	45.8	-0.4
47	41.6	-1.8
48	41.3	-1.9
49	44.9	-0.7
50	43.7	-1.1
51	45.2	-0.6
52	50.6	1.2	4:1s rule
53	50.3	1.1
54	51.2	1.4
55	51.5	1.5
56	44.3	-0.9
57	41.6	-1.8
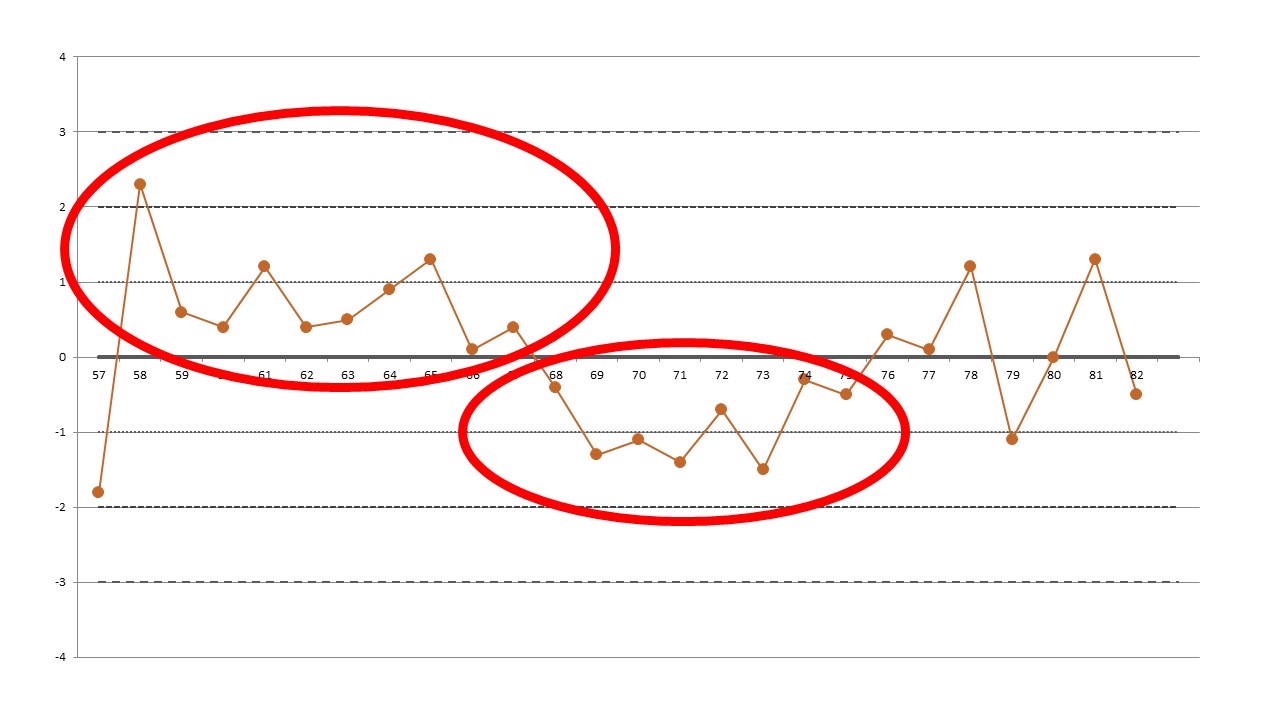
58	53.9	2.3	10:x rule
59	48.8	0.6
60	48.2	0.4
61	50.6	1.2
62	48.2	0.4
63	48.5	0.5
64	49.7	0.9
65	50.9	1.3
66	47.3	0.1
67	48.2	0.4
68	45.8	-0.4	8:x rule
69	43.1	-1.3
70	43.7	-1.1
71	42.8	-1.4
72	44.9	-0.7
73	42.5	-1.5
74	46.1	-0.3
75	45.5	-0.5
76	47.9	0.3
77	47.3	0.1
78	50.6	1.2
79	43.7	-1.1
80	47.0	0
81	50.9	1.3
82	45.5	-0.5

Remember the conditions:

We are only running ONE control per run; assume each value represents one run (this is not realistic from a US CLIA scenario, but we've got to start small)
We're NOT implementing the R:4s control rule, since we don't have two values that occur within a single run (which is the recommended interpretation for the R:4s rule)
We're NOT looking 2s violations. Let's break that habit right now. In any case, I didn't generate these data points randomly, so we're not going to expect to see a certain number of 2s outliers
We ARE going to try to find outliers of the following "Westgard Rules": 1:3s/2:2s/R:4s/4:1s/8:x (except remember the R:4s is not applicable)
We're NOT going to get into the swamp that is repeating of controls. So don't assume anything you see is a repeated control - just stick with "in" or "out"

The Charts

I suspect this is a very long table for most readers. And probably I'm asking quite a bit for readers to convert this chart into something like a levey-jennings chart. So we'll help out immediately by generating some Levey-Jennings control charts

Here are the first 27 data points:

Breeak all the Rules N=1, 1 through 27

Here are the second set of data points (from 32 through 56):

BreakAllTheRulesN1 Answer p32 56

Here's the last set of data points (57 through 82):

BreakAllTheRulesN1 ANSWERS p57 82

(Obviously, any data points not shown on these charts were automatically in-control.)

So, at the end of this, did you find the same answers?

9 different rule violations
- 2 violations of 1:3s rule
- 2 violations of 2:2s rule
- 2 violations of 4:1s rule
- 2 violations of 8:x rule
- 1 violation of 10:x rule
If only the "Westgard Rules" 1:3s/2:2s/R:4s were necessary for this method
- the 5 violations of 4:1s, 8:x, and 10:x would not have mattered (or we wouldn't have rejected the run based on those events)
If only the 1:3s control rule was necessary for this method
- the 8 other violations of 2:2s, 4:1s, 8:x, and 10:x would not have mattered (we wouldn't have rejected the run based on those events)

Tools, Technologies and Training for Healthcare Laboratories

Basic QC Practices