Sigma Metric Analysis
WBC on a SE 9500
Are things better or worse in hematology than in chemistry? Data from a recent AACC conference poster reveals more good news...
From Method Validation to Six Sigma metrics: A Hematology Example
- Recap: What do you need to go from Method Validation to Six Sigma?
- What calculations do you perform and in what order?
- Estimate Bias at the critical level of performance
- What's a Quality Requirement and where do I find it?
- Calculating Sigma Metrics from Bias, CV and Quality Requirement
- Conclusion
- Postscript: How would you QC this instrument?
 |
[Note: This QC application is an extension of the lesson From Method Validation to Six Sigma: Translating Method Performance Claims into Sigma Metrics. This article assumes that you have read that lesson first, and that you are also familiar with the concepts of QC Design, Method Validation, and Six Sigma. If you aren't, follow the links provided.] |  |
We are pleased to share the results of a user-submitted data set for White Blood Cells (WBC, leukocyte count) on a hematology instrument. Using the Basic Method Validation manual as a guide, they performed a comparison of methods experiment and a replication experiment. However, overwhelmed by the data that resulted, they asked us what the numbers meant, and if the new method was acceptable or not.
Recap: What do you need to go from method validation to Six Sigma?
From the Method Validation study, preferably performed in your laboratory. Otherwise, use the data provided by the manufacturer:
From other sources:
- Quality Requirement (CLIA, clinical, biologic or otherwise)
- Calculators (Six Sigma)
- Medical Decision Levels
- A QC Design tool (optional, but useful)
What data is available?
In this case, for WBC, the technologist had performed a Comparison of Methods study on 40 patient samples over the course of 2 days, comparing an SE-9500 method to an Alpha(TOA) method; and a Replication study on 20 samples of 3 controls (low, normal, and high) over the course of 20 days.
Comparison Study Results |
|
| slope | 1.01 |
| y-intercept | 0.19 |
| correlation coefficient, r | 0.99 |
The correlation coefficient is good - but remember, it is not sufficient grounds to judge that the method is acceptable. All the r tells you is that the the simple linear regression techniques are good enough to use for this comparison. If the r had been below 0.97 or 0.95, another method like Deming or Passing-Bablock regression would be better. More details about the use and interpretation of statistics are available on this website.
Replication Study Results |
|||
| Control | Low | Normal | High |
| mean | 2.949 | 6.405 | 17.065 |
| CV | 1.9 | 1.8 | 1.4 |
Again, by itself, the CV numbers are good but don't tell the whole story. Certainly, this is a between-day (across-run) replication study, so this is a CV that better reflects the variation in the method than a CV produced by a within-run or within-day replication study. And the fact that the between-day CV is still low is a good sign.
What calculations do I have to perform, and in what order?
- Use the regression equation to estimate bias at the level where performance is important.
- Find the quality requirement for that important level.
- Calculate Six Sigma metrics.
For our study, we'll use the Normal control level (6.405) as the critical level for performance. In the replication study, that CV is 1.8.
| Test Name | Level of interest | CV | Slope | Y-Int |
| WBC | 6.4055 | 1.8 | 1.01 | 0.19 |
Estimating Bias at the critical level of performance.
How do you do this? By using the Regression Equation:
Yc = a + b Xc where Yc and Xc represent the test and comparison values, respectively at a concentration level of interest, b is the slope, and a is the y-intercept. The slope and y-intercept are given from the comparison of methods experiment.
You use the critical level of performance as your Xc value. Then solve the Regression Equation for Yc. This will estimate what the value of the reference method will be at that level.
Next, take the value of Yc-Xc, and divide it by Xc. This provides an estimate of bias as a percentage.
At the end of these calculations, you have estimates of bias and CV at the same level.
Here’s what our example data looks like after we’ve performed these calculations:
y = 1.01(6.4055) + 0.19
y = 6.66
[(6.66 - 6.4055 ) / 6.4055 ] * 100 = 4.04% bias
| Test Name | Level of Interest | CV | Bias % |
| WBC | 6.4055 | 1.8 | 4.04% |
Note that even after those calculations, it’s still difficult to judge the quality of this method.
What’s a quality requirement and where do I find it?
Finding or defining quality requirements is a critical step in the QC Design Process. We refer you to those articles on the website for more explanation. Since we are working with a chemistry instrument, we are in luck. CLIA has defined the quality requirements for all the WBC test (leukocyte count). Let’s add that to our table:
| Test Name | Level of Interest | Quality Requirement |
CV | Bias % |
| WBC | 6.4055 | 15% | 1.8 | 4.04% |
Now that we’ve added the quality requirement, we’re ready to get Six Sigma metrics! We’ll really be able to see how this test stands up.
Calculating Sigma Metrics from Bias, CV and Quality Requirement.
Again, the website has already covered the relationship between Six Sigma Metrics and bias, CV, and quality requirements. There is even a free online calculator on Westgard Web to perform the caculations.
Let’s see the Sigma Metric:
The basic equation is this:
(Quality Requirement - Bias ) / CV = Sigma metric
[either all terms in units or all terms in percentages as the case is here]
In our example:
(15 - 4.04) / 1.8 = 6.09
| Test Name | Level of Interest | Quality Requirement |
CV | Bias % | Sigma metric |
| WBC | 6.4055 | 15% | 1.8 | 4.04% | 6.09 |
Here we see that the goal of Six Sigma has been achieved. This method is performing nearly defect-free. Our professional advice at this point is to celebrate.
Conclusion: For WBC in this lab, Six Sigma is within reach
For many methods in the healthcare laboratory, defect-free operation is possible. With low bias and CVs, these methods could eliminate unncessary defects.
Postscript: How would you QC this instrument?
For a moment, let’s assume that you have this instrument and you’ve finished celebrating. Does a metric of Six Sigma mean that you're never going to see an out-of-control result? Unfortunately, NO. Errors will still occur, not only due to random factors, including human error (using the wrong control), but also during control lot switches, calibration times, etc. There are still problems that will occur when the instrument becomes "unstable." But under stable performance, there should be very few defects.
But even during stable performance, you may get out-of-control flags due to "noise" or false rejection. Your choice of control rule at this point will determine how many false rejections (false alarms) you can expect to encounter. When a method has a Sigma metric of 6 or higher, the out-of-control flags you see will often be due to false rejection, not real errors. The goal with six Sigma metric methods is to use control rules that reduce the false rejection to as few as possible.
For Sigma metrics above 3 sigma, we recommend using a QC Design or QC Planning tool like the Normalized OPSpecs charts available on the website, or EZ Rules®.
[ For methods below 3 sigma, you want to use the "full Westgard Rules" with as many controls as you can afford. 13s/22s/R4s/41s/8x for example, with 4 control measurements or more. ]
Below is a screenshot from EZ Rules®, using a Sigma Metics graph to illustrate the performance of the method and the many possible control rule choices. Along the right side of the screen you can see a list of the control rules, as well as their error detection (Ped) and false rejection (Pfr) capabilities:
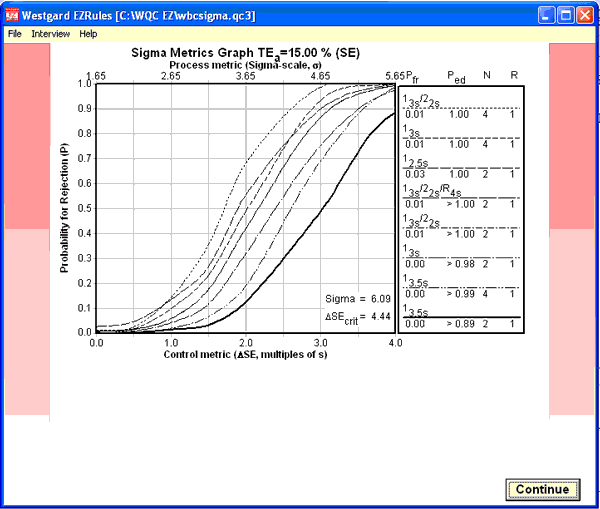
The Automatic QC Selection function of EZ Rules® has selected a 13.5s with 2 control measurements per run. However, a 13s rule with 2 control measurements per run would also provide greater than 98% error detection of critically-sized errors, while providing essentially zero false rejection.
[ Note: If you were using the traditional 2s limits with 2 controls, you would expect to encounter 9% false rejections. That's nearly 1 out of 10 runs you would reject for no reason. On a method that is virtually defect-free, you definitely don't want to spend 1 out of every 10 runs trying to figure out if something is wrong. ]
